Proposition 8

Let a straight line AB be cut at random at the point C.

I say that four times the rectangle AB by BC plus the square on AC equals the square described on AB and BC as on one straight line.

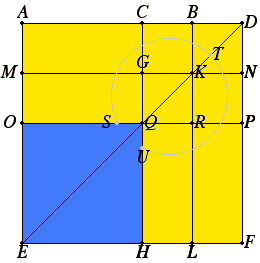
Produce the straight line BD in a straight line with AB, and make BD equal to CB. Describe the square AEFD on AD, and let the figure be drawn.

Then, since CB equals BD, while CB equals GK, and BD equals KN, therefore GK also equals KN.

For the same reason QR also equals RP.

And, since BC equals BD, and GK equals KN, therefore CK also equals KD, and GR equals RN.

But CK equals RN, for they are complements of the parallelogram CP. Therefore KD also equals GR. Therefore the four areas DK, CK, GR, RN equal one another. Therefore the four are quadruple of CK.

Again, since CB equals BD, while BD equals BK, that is CG, and CB equals GK, that is GQ, therefore CG also equals GQ.

And, since CG equals GQ, and QR equals RP, AG also equals MQ, and QL equals RF.

But MQ equals QL, for they are complements of the parallelogram ML, therefore AG also equals RF. Therefore the four areas AG, MQ, QL, RF equal one another. Therefore the four are quadruple of AG. But the four areas CK, KD, GR, RN were proved to be quadruple of CK, therefore the eight areas, which contain the gnomon STU, are quadruple of AK.

Now, since AK is the rectangle AB by BD, for BK equals BD, therefore four times the rectangle AB by BD is quadruple of AK.

But the gnomon STU was also proved to be quadruple of AK, therefore four times the rectangle AB by BD equals the gnomon STU.

Add OH, which equals the square on AC, to each. Therefore four times the rectangle AB by BD plus the square on AC equals the gnomon STU plus OH.

But the gnomon STU and OH are the whole square AEFD, which is described on AD. Therefore four times the rectangle AB by BD plus the square on AC equals the square on AD.

But BD equals BC.

Therefore four times the rectangle AB by BC together with the square on AC equals the square on AD, that is to the square described on AB and BC as on one straight line.

Therefore if a straight line is cut at random, then four times the rectangle contained by the whole and one of the segments plus the square on the remaining segment equals the square described on the whole and the aforesaid segment as on one straight line.