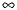 . Thus, we have a correspondence between the plane with a point of infinity with the sphere.
. Thus, we have a correspondence between the plane with a point of infinity with the sphere.
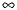 , is not treated separately, the ordinary Euclidean plane is replaced by the sphere. This is most easily seen by means of the well-known stereographic projection.
A nice feature of using the sphere is that straight lines in the Euclidean plane correspond to circles on the sphere, so that straight lines and circles are put on the same footing. Furthermore, reflecting across a straight line becomes inversion in a circle on the sphere.
, is not treated separately, the ordinary Euclidean plane is replaced by the sphere. This is most easily seen by means of the well-known stereographic projection.
A nice feature of using the sphere is that straight lines in the Euclidean plane correspond to circles on the sphere, so that straight lines and circles are put on the same footing. Furthermore, reflecting across a straight line becomes inversion in a circle on the sphere.
Here's how it works. Take a sphere and a plane in three-space. Typically, the plane is taken to cut through the center of the sphere, or it's taken tangent to the sphere, but it doesn't matter. What's important is the selection of the projection point N. It must be on the sphere and on a line through the center of the sphere perpendicular to the given plane. (It also can't be a point in the plane.) In this diagram, the sphere is tangent to the plane at the point S (south pole), O is the center of the sphere, and N (north pole) is the projection point.
A point A on the sphere corresponds to a point B on the plane when the three points N, A, and B are collinear. The only point on the sphere that doesn't correspond to a point in the plane is the projection point N, and it corresponds to the point at infinity, 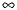 . Thus, we have a correspondence between the plane with a point of infinity with the sphere.
. Thus, we have a correspondence between the plane with a point of infinity with the sphere.
It's fairly easy to see why a straight line in the plane, like BD, corresponds to a circle on the sphere passing through the projection point N. Just consider the plane that includes the line BD and the point N. It will cut the sphere in a circle ACN. Conversely, given a circle ACN passing through the projection point N, the plane of the circle will intersect the base plane in a line BD.
It is more difficult to see why a cirle in the plane corresponds to a circle on the sphere not passing through the projection point N. In the diagram below, we'll show that the circle ACE on the sphere is projected to the circle BDF on the plane.
The easiest way to see that is to recognize stereographic projection as an inversion in a sphere. Inversions in a sphere are three-dimensional analogues of inversions in a circle. The defining proportion is the same.
Inversion in a sphere has properties similar to inversion in a circle. For instance, inverting a sphere A in a sphere B results in a sphere A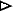 B, unless the center of the B sphere lies on A, in which case the result is a plane.
B, unless the center of the B sphere lies on A, in which case the result is a plane.
Take the first case where the center P of B doesn't lie on the the sphere A. The sphere Ais generated by rotating a circle around an axis, so take the axis to be line OP connecting the centers P and O of the spheres. Then the sphere A intersects that axis at two points C and D, and A is the sphere on the diameter CD.
Let a plane containing this axis rotate around the axis. That plane intersects A in a circle with diameter CD, and the inverse of that circle is the circle in that plane on the diameter C'D', where C' and D' are the points inverse to C and D, respectively. As the plane rotates around the axis, the circles on the diameter CD are inverted to the circles on the diameter C'D'. Thus, a sphere A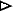 B is generated by the rotating inverse circles.
B is generated by the rotating inverse circles.
The other case where the center of B does lie on A is relevant to stereographic projection. The argument that A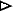 B is a plane is similar to the previous argument, but it depends on the fact that a plane is generated by a rotating line perpendicular to an axis at a point on that axis.
B is a plane is similar to the previous argument, but it depends on the fact that a plane is generated by a rotating line perpendicular to an axis at a point on that axis.
We'll show now that the stereographic projection of a sphere with diameter NS to the plane tangent to S is actually inversion in a sphere with center N and radius NS. The diagram to the left shows a cross section, that is, an intersection with a plane containing the axis NS. The point A on the sphere is projected to the point B. Note that we have three similar right triangles: NSB, NAS, and SAB. Therefore, NA : NS = NS : AB. Thus, when A is inverted in the circle with radius NS, the resulting point is B. We conclude that stereographic projection is inversion in a sphere.
Now we can answer why stereographic projection preserves circles. Consider any circle on the sphere that doesn't pass through N. It is the intersection of the sphere with a plane.
Since stereographic projection is an inversion in a circle, that plane will be inverted to a sphere , and that sphere will intersect the tangent plane is a circle. Thus the image of a circle not passing through N is a circle.
March, 2002.
David E. Joyce
Department of Mathematics and Computer Science
Clark University
Worcester, MA 01610
Email: djoyce@clarku.edu
My Homepage