 |
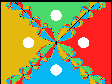
The polynomial z4 - 1 has roots at 1, i, -1, and -i. White dots are placed around the roots. |
 |
The polynomial z3 - 1 has the three roots of unity as its roots. The three roots are 1 (of course), -0.5 + 0.86603 i, and -0.5 - 0.86603 i. |
| This and the last example are specific cases of the n-th roots of unity. They are the roots of the polynomial zn - 1. The n roots are equally spaced around the unit circle (that is, the circle whose equation is x2 + y2 = 1), so their coordinates can easily be given in terms of cosines and sines. The angles for these n points as measured counterclockwise from the positive x-axis are
0°, 360°/n, 360°·2/n, ..., 360° (n-1)/n,
the k-th of these angles being 360° k/n. Therefore, the k-th root is
cos (360° k/n) + i sin (360° k/n).
In particular, the 0-th root is 1 itself.
|
 |
Even when the roots are all real, the Newton basins in the complex plane are interesting. In this example, the polynomial is z3 - z, and its roots are -1, 0, and 1. |
 |
Here's an example where all the roots are complex but come in pairs.
The six roots are ±(1+3i), ±(5+i), and ±(3-2i). The sixth degree polynomial is (z2 - (1+3i)2)(z2 - (5+i)2)(z2 - (3-2i)2). |
 |
The polynomial (z4 - 1)(z4 + 16), that is,
z8 + 15z4 - 16, has eight roots: ±1, ±i, ±(1+i), and ±(1-i).
The roots are at the corners and the midpoints of the sides of the displayed square. |
 |
This polynomial (z4 - 1)(z2 - (1+i)2) has six roots: ±1, ±i, and ±(1+i).
The lighter colors indicate fewer iterations of Newton's method before the approximations are close to the roots. |
 |
The polynomial (z2 + 4z + 1)(z2 +4)(z - 2), that is, z5 + 2z4 - 3z3 + 6z2 - 28 z - 8,
has five roots: 2+i, 2-i, 2i, -2i, and -2.
|
 |
The polynomial (z4 - 1)(z4 - 16), that is,
z8 - 17z4 + 16, has eight roots: ±1, ±i, ±2, and ±2i. |
 |
Looking at the examples so far you'll get the impression that Newton's method almost always works. But sometimes that isn't so. Here's an example of a cubic polynomial for which lots of initial guesses never get close to any solution. Those initial guesses are colored black.
|
 |
The cubic polynomial for this image has two of the same roots as the last polynomial, but the third is slightly moved. The black area is a much more interesting shape. |