Newton Basins
Newton's method
David E. Joyce
Clark University
August, 1994
Although you can enjoy the Newton Basin images without knowing the
technical basis for them, it helps to understand it.
Newton's method for finding roots of functions.
Newton's method began as a method to approximate roots of functions,
equivalently, solutions to equations of the form f(x)=0. Not only is the method easy
to comprehend, it is a very efficient way to find the solution to the equation.
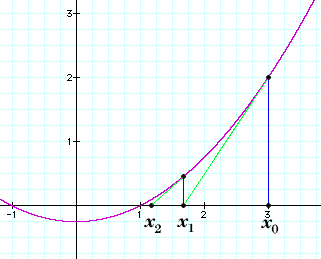 Suppose you start with a value x0 that you think
might be close to a root. The line tangent to the curve y=f(x) through the
point (x0, f(x0)) is pretty close to the curve, so
wherever that line crosses the x-axis should be very close to the root. Since the slope of
the curve is the derivative f'(x0), that point of intersection is easy to
compute; the point's x-value is
Suppose you start with a value x0 that you think
might be close to a root. The line tangent to the curve y=f(x) through the
point (x0, f(x0)) is pretty close to the curve, so
wherever that line crosses the x-axis should be very close to the root. Since the slope of
the curve is the derivative f'(x0), that point of intersection is easy to
compute; the point's x-value is
So, a better approximation than
x0 ought to be
x1. Now, if that's not close enough for you, use the method again on
x1 to get a better approximation x2:
Iterate the method until
you're satisfied.
For a lot of functions, this iterative method works very well.
But not for all functions. For instance, it doesn't work for any function that doesn't have a root.
How could it? And it doesn't always work for some functions that do have roots, for instance, the
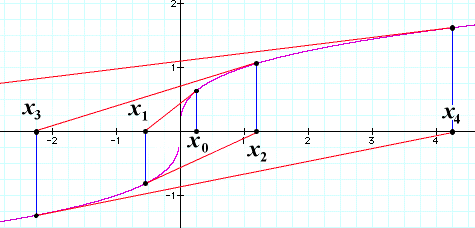
cube root function. If you look for the root of the function f(x) =
x1/3 with any initial value, your estimates won't converge. The graph shows how
with in initial estimate x0 near 0, the subsequent estimates x1,
x2, and so forth, run off to infinity!
Even for those functions it does work for, you might choose a bad initial point x0.
For instance, f'(x0) might be zero. Still, it's pretty good, and there are
various criteria to tell when it's going to work at all.
Newton's method and complex numbers: Newton basins
The method works for complex functions, too.
For more information on complex numbers, see
Dave's Short Course on Complex Numbers.
For a complex-valued function f(z)
whose argument z is complex, you can get better approximations to the root by replacing an
initial approximation z0 by the next approximation using the same formula as before:
Exceptions occur for complex functions as they do for initial functions.
Now, a function can have several roots. A polynomial of degree
n has n roots. That's the "fundamental theorem of algebra." Of course, you have to
count multiplicities of roots, and you have to allow complex roots as well as real roots.
The question is: which root do you approach when you start with an initial value? If you start close
to a root, then Newton's method brings you closer to the root faster and faster. But if you start
far from a root, then Newton's method may take you to some root other than the closest one. Suppose
you paint the complex plane in colors so that all the points that approach a particular root are
painted one color. We'll say those points lie in one Newton basin for the function. An interesting
pattern emerges. (A few points won't approach any root. Don't color them any color.)
Up to the Introduction
On to some Examples
copyright © 1994, 1997.
The address of this file is http://aleph0.clarku.edu/~djoyce/newton/newton.html