Proposition 10
To bisect a given finite straight line.
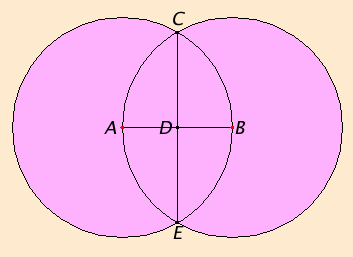
Let AB be the given finite straight line.
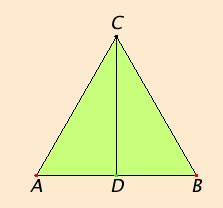
It is required to bisect the finite straight line AB.
Construct the equilateral triangle ABC on it, and bisect the angle ACB by the straight line CD.
I say that the straight line AB is bisected at the point D.
Since CA equals CB, and CD is common, therefore the two sides CA and CD equal the two sides CB and CD respectively, and the angle ACD equals the angle BCD, therefore the base AD equals the base BD.
Therefore the given straight line AB is bisected at D.
Q.E.F.