Proposition 20
In any triangle the sum of any two sides is greater than the remaining one.
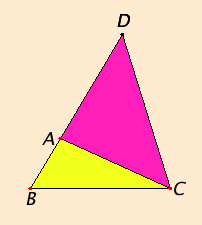
Let ABC be a triangle.
I say that in the triangle ABC the sum of any two sides is greater than the remaining one, that is, the sum of BA and AC is greater than BC, the sum of AB and BC is greater than AC, and the sum of BC and CA is greater than AB.
Draw BA through to the point D, and make DA equal to CA.
Join DC.
Since DA equals AC, therefore the angle ADC also equals the angle ACD. Therefore the angle BCD is greater than the angle ADC.
Since DCB is a triangle having the angle BCD greater than the angle BDC, and the side opposite the greater angle is greater, therefore DB is greater than BC.
But DA equals AC, therefore the sum of BA and AC is greater than BC.
Similarly we can prove that the sum of AB and BC is also greater than CA, and the sum of BC and CA is greater than AB.
Therefore in any triangle the sum of any two sides is greater than the remaining one.
Q.E.D.
Guide
This proposition is known as the triangle inequality. It is part of the statement that the shortest path between two points is a straight line. With this proposition you can show that among all polygonal paths between two points, the shortest one is the one that consists of a single line joining the two points. There are, of course, many other conceivable paths besides polygonal paths.
A minimum distance
This proposition on the triangle inequality, along with I.15 on vertical angles, allows us to solve a problem on minimum distance, described and solved by Heron of Alexandria (ca. 10–ca. 70).
|
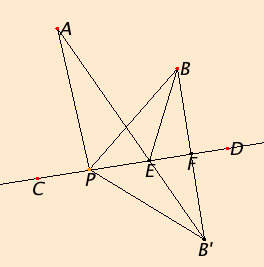
Suppose there are two points A and B on the same side of a line CD. The problem is to find the shortest path which goes first from the point A to some point P on the line CD, then from P to the point B. We will only consider paths that are made out of straight lines; call such a path a bent line. But that still leaves us the question of which point P to choose on the line CD to minimize the sum of the distances AP plus PB.
The solution is that the shortest path will be the path AEB where angle of incidence, namely, angle AEC, equals the angle of reflection, namely, angle BED.
First, we should show how to construct the bent line where the angle of incidence equals the angle of reflection. Draw a perpendicular BF from the point B to the line CD (I.12), and extend it to B' so that FB' = BF (I.Post.2, I.3). Draw AB' and let E be the point where AB' intersects CD. (There will be a point of intersection since A and B' are on opposite sides of CD.) Draw BE.
|
|
Now, triangles BFE and B'FE are congruent since they have two sides and the included angle equal (I.4), the included angles being right angles. Therefore, angles BFE and BF'E are equal. The vertical angle AEC across from angle B'ED also equals these angles (I.15). Thus, the angle of incidence AEC equals the angle of reflection BED.
We still have to show that the distance AE + EB is less than any distance AP + EP for any point P other than E that lies on the line CD. Let P be such a point and draw lines AP, BP, and B'P. Then by proposition I.20, above, AP + EP is less than AB'. But AB' = AE + EB', and EB' = EB,
therefore AP + EP is less than AE + EB.
Thus, the shortest bent line between two points on the same side of a line that meets that line is the one where the angle of incidence equals the angle of reflection.
Q.E.D.
Use of Proposition 20
This proposition is used in the next two propositions, several in Book III, and XI.20.