Proposition 45
Let ABCD be the given rectilinear figure and E the given rectilinear angle.
It is required to construct a parallelogram equal to the rectilinear figure ABCD in the given angle E.
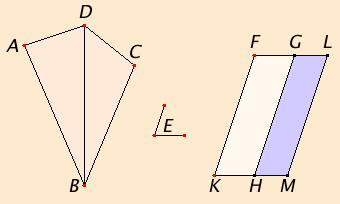
Join DB. Construct the parallelogram FH equal to the triangle ABD in the angle HKF which equals E. Apply the parallelogram GM equal to the triangle DBC to the straight line GH in the angle GHM which equals E.
Since the angle E equals each of the angles HKF and GHM, therefore the angle HKF also equals the angle GHM.
Add the angle KHG to each. Therefore the sum of the angles FKH and KHG equals the sum of the angles KHG and GHM.
But the sum of the angles FKH and KHG equals two right angles, therefore the sum of the angles KHG and GHM also equals two right angles.
Thus, with a straight line GH, and at the point H on it, two straight lines KH and HM not lying on the same side make the adjacent angles together equal to two right angles, therefore KH is in a straight line with HM.
Since the straight line HG falls upon the parallels KM and FG, therefore the alternate angles MHG and HGF equal one another.
Add the angle HGL to each. Then the sum of the angles MHG and HGL equals the sum of the angles HGF and HGL.
But the sum of the angles MHG and HGL equals two right angles, therefore the sum of the angles HGF and HGL also equals two right angles. Therefore FG is in a straight line with GL.
Since FK is equal and parallel to HG, and HG equal and parallel to ML also, therefore KF is also equal and parallel to ML, and the straight lines KM and FL join them at their ends. Therefore KM and FL are also equal and parallel. Therefore KFLM is a parallelogram.
Since the triangle ABD equals the parallelogram FH, and DBC equals GM, therefore the whole rectilinear figure ABCD equals the whole parallelogram KFLM.
Therefore the parallelogram KFLM has been constructed equal to the given rectilinear figure ABCD in the angle FKM which equals the given angle E.