Proposition 9
Let the angle BAC be the given rectilinear angle.
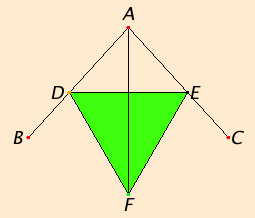
It is required to bisect it.
Take an arbitrary point D on AB. Cut off AE from AC equal to AD, and join DE. Construct the equilateral triangle DEF on DE, and join AF.
I say that the angle BAC is bisected by the straight line AF.
Since AD equals AE, and AF is common, therefore the two sides AD and AF equal the two sides EA and AF respectively.
And the base DF equals the base EF, therefore the angle DAF equals the angle EAF.
Therefore the given rectilinear angle BAC is bisected by the straight line AF.
Guide
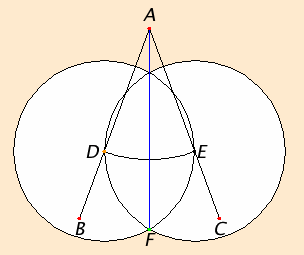
Construction stepsWhen using a compass and a straightedge to perform this construction, three circles and the final bisecting line need to be drawn. One circle with center A and radius AD is needed to determine the point E. The other two circles with centers at D and E and common radius DE intersect to give the point F. The sides of the equilateral triangle aren’t needed for the construction.There is an alternate construction where the circles centered at D and E have a different radius, namely, AD, which equals AE. A different proof is required to show that this alternate construction works. |
|
On angle trisection
Angle bisection is an easy construction to make using Euclidean tools of straightedge and compass. Also, line bisection is quite easy (see the next proposition I.10), and division of a line into any number of equal parts is not especially difficult (see proposition VI.9).Dividing an angle into an odd number of equal parts is not so easy, in fact, it is impossible to trisect a 60°-angle using Euclidean tools (the Postulates 1 through 3). Euclid’s predecessors employed a variety higher curves for this purpose. Archimedes, after Euclid, created two constructions: his spiral could divide an angle into any number of parts, and his neusis construction could trisect angles (see the note on I.Post.2). By Pappus’ time it was believed that angle trisection was not possible using Euclidean tools, but that wasn’t proven until 1837 when Wantzel (1814–1838) published his proof.
Nevertheless, amateur geometers continue to search in vain for such a construction and frequently bother mathematicians with their purported solutions. Their solutions are of two forms. Sometimes they simply construct approximate trisections. Other times they use neusis or some other other tool that goes beyond Euclid’s tools.
Students of geometry are cautioned not to waste their time on this problem and, if they do, not to bother others with their purported solutions. Much better would be to study Galois theory, the mathematics that proves the impossibility of angle trisection.