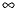 to the plane, and let O and
to the plane, and let O and 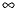 be inverses of each other.
be inverses of each other.
Fix a circle with center O and radius OA = r. For each point P other than the center O, the point inverse to P in the circle O is that point P' on the line OP (extended in the direction of P if needed) so that the proportion
is satisfied. An equivalent condition is that
In order to cover the special case that occurs when P is the center
O of the circle, we'll add a point 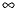 to the plane, and let O and
to the plane, and let O and 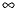 be inverses of each other.
be inverses of each other.
We'll use the notation P C to indicate the inverse point P'. Read "P
C to indicate the inverse point P'. Read "P C" as "P through
C." More generally, when B is any plane geometric figure (point, line, circle, etc.) and C is a circle,
we'll use the notation B
C" as "P through
C." More generally, when B is any plane geometric figure (point, line, circle, etc.) and C is a circle,
we'll use the notation B C for the result of inverting B in the circle C.
We'll also use this notation for reflecting across a straight line. So, if B is any plain geometric figure, and L
is a straight line, then B
C for the result of inverting B in the circle C.
We'll also use this notation for reflecting across a straight line. So, if B is any plain geometric figure, and L
is a straight line, then B L is the figure that results from reflecting B across
L.
L is the figure that results from reflecting B across
L.
Note that inversion in a circle is an involution. That is, application of inversion in the same circle a second
time undoes the first application. Otherwise said, it is an operation that when done twice yields the identity operation.
Algebraically, this observation is the identity (B C)
C) C =
B,
where B is any plane figure.
C =
B,
where B is any plane figure.
Also note that a point P is its own inverse, that is, P C = P, if and only if it lies on the circumference of the circle. In particular, C
C = P, if and only if it lies on the circumference of the circle. In particular, C C = C.
C = C.
The standard construction to invert a point in a circle uses both compass and
straightedge, so we won't be able to use it. Our construction using just a compass will come later. Still, the standard
construction is interesting. We only need to consider points P which either lie outside the circle, or lie inside the
circle but are not the center of the circle; points on the circle are their own inverses, and the center has 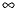 as its inverse.
as its inverse.
Let there be a circle with center O and radius OA = r, and let P be a point. To invert P in the circle, first draw the line OP. Now, if P happens to be a point outside the circle, then draw the tangents PB and PC to the circle, then draw the line BC. Where these two lines meet will be the inverse point P'. Since the two right triangles OBP and BP'P are similar, therefore the proportion OP / r = r / OP' holds.
But if P happens to be a point inside the circle (except the center), then draw the line BC perpendicular to OP, and let B and C be the points of intersection of that line with the circle. Then draw tangents to the circle at B and C. In this case, the inverse point P' is the intersection of the two tangent lines. Note again the two similar right triangles, from which it follows that the identical proportion holds.
A third case occurs when P lies on the circle, and in that case let the inverse point P' be the same as P itself.
The fourth case occurs when P is the center O of the circle, and as mentioned
above, O and 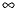 are inverses.
are inverses.
We will invert lines and circles in our circle with center O and radius OA = r.
First, consider a line BC which doesn't pass through the center O. We'll show that its inverse is a circle passing through the center of the circle. Let D be the foot of the perpendicular drawn from O to the line BC. Let D' be the point inverse to D. Draw the circle with diameter OD'. Let E be an arbitrary point on the line BC, and let E' be where the ray OE meets the circle with diameter OD'. Then triangle OE'D' is a right triangle, and it's similar to the right triangle ODE. Hence, we have the proportion
Since inversion is an involution, it is clear that any circle passing through the center of our circle will invert to a straight line.
Should a line BC pass through the center O, then it is clear that its inverse will be itself.
We'll start with the case where O lies outside the circle BCD.
Let E be any point on the circle BCD, and F the other point where the line OE intersects the circle BCD. Let OT be a line from O tangent to the circle BCD at the point T, and let t denote the length OT. Then by Euclid's Proposition III.35, OE OF = t2.
We're looking for a point E' on the line OE such that OE OE' = r2. Dividing this equation by the equation OE OF = t2, we recognize that what we need is a point E' so that
Therefore, OE' is a constant times OF. This means that when we apply a scaling to the plane by a factor of t2 / r2 with the fixed point of the plane being O, then points on the circle BCD will be inverted to points in the scaled circle. Note that both the original and scaled circles have the same tangent lines from the point O.
The other case occurs when O lies inside the circle BCD. It may seem that because there are no tangents from O to the circle BCD we've run into serious problems. But we didn't actually use the tangent lines in the first case; all we needed to know was that the product OE OF was a constant. In this case, it's also a constant.
As before, let E be any point on the circle BCD, and F the other point where the line OE intersects the circle BCD. (This time, F is on the other side of O.) Then by Euclid's Proposition III.36, the product OE OF is a constant, call it k.
We're still looking for a point E' on the line OE such that OE OE' = r2. Dividing this equation by the equation OE OF = k, we recognize that what we need is a point E' so that
Therefore, OE' is a constant times OF. This means that when we apply a scaling to the plane by a factor of k / r2 with the fixed point of the plane being O, then points on the circle BCD will be inverted to points in the scaled circle.
We conclude that when one circle is inverted in another, and the center of the other is not on the circumference of the first, then the result is a circle. But if the center of the other is on the circumfere nce of the first, then the result is a straight line.
Now examine what happens to
the inverted point D = B OT of a point B in the circle OT as the circle
enlarges. In the diagram, as you drag point A toward S, the circle OT approaces the line ST and the
inverse point D approaches C = B
OT of a point B in the circle OT as the circle
enlarges. In the diagram, as you drag point A toward S, the circle OT approaces the line ST and the
inverse point D approaches C = B ST, the reflection of C in the line
ST. Thus, the operation of reflection in a line is a limit of inversions in circles.
ST, the reflection of C in the line
ST. Thus, the operation of reflection in a line is a limit of inversions in circles.
March, 2002.
David E. Joyce
Department of Mathematics and Computer
Science
Clark University
Worcester, MA 01610
Email: djoyce@clarku.edu
My Homepage