Compass Geometry
6. Construction C to find the center of a circle given three points on its circumference
We're not done yet in showing that compasses alone are sufficient to construct all the constructable points in Euclidean geometry. The problem is that all the circle constructions depend on knowing the centers of the circles, and when we invert one circle C in another D to get a circle E = C D, then the center of E is not the inverse of the center of C inverted in D. The center of E is determined, however, by three of the points on E, and three points on E can by found by taking any three points on C and inverting them in D. Thus, we'll need the construction C to find the center of a circle given three points on its circumference.
D, then the center of E is not the inverse of the center of C inverted in D. The center of E is determined, however, by three of the points on E, and three points on E can by found by taking any three points on C and inverting them in D. Thus, we'll need the construction C to find the center of a circle given three points on its circumference.
Let P,Q, and R be three given points. We are to construct the center O of the circle passing through them. We'll find O by inverting everything in the circle C with center P and radius PQ.
First, invert the point R in C to get the point R' = R C.
Next draw two circles, one with center Q and radius QP, the other with center R' and radius R'P. Besides at P, these two circles will intersect at another point O'. It is evident that this point O' is the reflection of P in the line QR', that is, O' = P
C.
Next draw two circles, one with center Q and radius QP, the other with center R' and radius R'P. Besides at P, these two circles will intersect at another point O'. It is evident that this point O' is the reflection of P in the line QR', that is, O' = P QR'. Finally, invert O' in C to get O.
QR'. Finally, invert O' in C to get O.
Next, we'll show O is the center of the circle PQR. Now, when the circle PQR is inverted in the circle C, then the result is the straight line QR', since P will be sent to the point 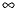 at infinity, Q is fixed, and R is sent to R'. Algebraically, that says PQR
at infinity, Q is fixed, and R is sent to R'. Algebraically, that says PQR C = QR'. To show that O is the center of the circle PQR, we only need to show that O =
C = QR'. To show that O is the center of the circle PQR, we only need to show that O =
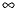
 PQR. That will follow from a property of
PQR. That will follow from a property of  , namely,
, namely,  distributes over itself on the right, as shown in the next section.
distributes over itself on the right, as shown in the next section.
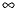
 PQR =
(P
PQR =
(P C)
C)  (QR'
(QR' C) =
(P
C) =
(P QR')
QR') C =
O'
C =
O' C = O.
C = O.
Thus, we have constructed O, the center of the circle passing through the three points P, Q, and R.
Next part: 7. Involutory quandles
March, 2002.
David E. Joyce
Department of Mathematics and Computer Science
Clark University
Worcester, MA 01610
Email: djoyce@clarku.edu
My Homepage
 C.
Next draw two circles, one with center Q and radius QP, the other with center R' and radius R'P. Besides at P, these two circles will intersect at another point O'. It is evident that this point O' is the reflection of P in the line QR', that is, O' = P
C.
Next draw two circles, one with center Q and radius QP, the other with center R' and radius R'P. Besides at P, these two circles will intersect at another point O'. It is evident that this point O' is the reflection of P in the line QR', that is, O' = P QR'. Finally, invert O' in C to get O.
QR'. Finally, invert O' in C to get O.
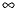 at infinity, Q is fixed, and R is sent to R'. Algebraically, that says PQR
at infinity, Q is fixed, and R is sent to R'. Algebraically, that says PQR