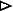 C. Draw the circle with center P and radius
PO. Then this new circle meets the circle C at two points, Q and Q'.
Draw the two circles with centers Q and Q' and radii QO and QO',
respectively. Besides O, they will meet at another point P'.
C. Draw the circle with center P and radius
PO. Then this new circle meets the circle C at two points, Q and Q'.
Draw the two circles with centers Q and Q' and radii QO and QO',
respectively. Besides O, they will meet at another point P'.
The geometry of compasses was developed independently by G. Mohr in Denmark in 1672, and by L. Mascheroni in Italy in 1797. The easiest way, however, to show that compasses are sufficient depends on circle inversion which wasn't invented until 1828 by Jacob Steiner.
References: R. Courant and H.E. Robbins, What is Mathematics? Oxford Univ. Pr., New
York, 1953.
H.S.M. Coxeter, Introduction to Geometry, Wiley, New York, 1961.
D. Pedoe, Circles, Dover, New York, 1957.
There are three methods to construct points in Euclidean geometry.
It is evident that the first construction is possible by compasses alone; just draw the two circles. The other two constructions will be possible if we can show that we can invert points in circles with compasses alone, and find centers of circles. Those are the constructions
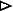 C for the result of inverting A in the
circle C.
C for the result of inverting A in the
circle C.
Let there be given a circle C with center O and point A on its circumference,
and a point P either outside the circle C or inside but more than half the radius away
from O. Here is a construction to invert P in the circle to get P' =
P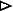 C. Draw the circle with center P and radius
PO. Then this new circle meets the circle C at two points, Q and Q'.
Draw the two circles with centers Q and Q' and radii QO and QO',
respectively. Besides O, they will meet at another point P'.
C. Draw the circle with center P and radius
PO. Then this new circle meets the circle C at two points, Q and Q'.
Draw the two circles with centers Q and Q' and radii QO and QO',
respectively. Besides O, they will meet at another point P'.
Then the two triangles QOP and P'OQ are each isosceles, and they have the same base angles, so they're similar. Therefore OP:OQ = OQ:OP'. Thus, P' is the inverse of P in the original circle C.
Now, this construction doesn't work if P is within half the radius of O since the two
circles won't intersect to produce the points Q and Q', so some other construction is
needed to invert such P. If P is at least a quarter of the radius away from O,
then we can easily find the point R twice as far from O as P is, then invert
R in the circle C to get R' = R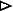 C by the
method described above, and then P' will be the point twice as far from O as R'
is. The doubling construction
C by the
method described above, and then P' will be the point twice as far from O as R'
is. The doubling construction
Now we can invert a point P in a circle at least a quarter of a radius away from the center.
When P is very close to O, all we have to do is repeatedly double the distance from O until we've got a point at least half the radius from O, invert that point, and double the resulting distance the same number of times to get P'.
We can trisect OP by doubling OP to OR then doubling PR to PS, so that OS is triple OP, then inverting S in the circle with center O and radius OP to get S'. Then OS' will be one-third of OP
More generally, we can cut off an n-th of OP by first extending OP by a factor of n, then inverting in that same circle.
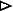 D, then the center of E is not the inverse
of the center of C inverted in D. The center of E is determined, however, by
three of the points on E, which can by found by taking any three points on C and
inverting them in D. Thus, we'll need the construction C to find the center of a
circle given three points on its circumference.
D, then the center of E is not the inverse
of the center of C inverted in D. The center of E is determined, however, by
three of the points on E, which can by found by taking any three points on C and
inverting them in D. Thus, we'll need the construction C to find the center of a
circle given three points on its circumference.
Let P, Q, and R be three given points. We are to construct the center O of the circle passing through them. We'll find O by inverting everything in the circle C with center P and radius PQ.
First, invert the point R in C to get the point R' = R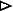 C.
Next draw two circles, one with center Q and radius QP, the other with center R'
and radius R'P. Besides at P, these two circles will intersect at another point
O'. This point O' is the reflection of P in the line QR', that is,
O' = P
C.
Next draw two circles, one with center Q and radius QP, the other with center R'
and radius R'P. Besides at P, these two circles will intersect at another point
O'. This point O' is the reflection of P in the line QR', that is,
O' = P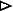 QR'. Finally, invert O' in C to
get O.
QR'. Finally, invert O' in C to
get O.
Now when the desired circle PQR is inverted in the circle C, then the result is the
straight line QR', since P will be sent to the point at infinity, 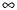 . Algebraically, PQR
. Algebraically, PQR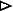 C = QR'. We can
now show that O is the center of the circle PQR, that is, O =
C = QR'. We can
now show that O is the center of the circle PQR, that is, O =
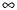
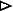 PQR.
PQR.
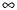
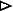 PQR =
(P
PQR =
(P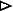 C)
C) 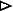 (QR'
(QR'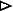 C) =
(P
C) =
(P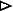 QR')
QR')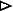 C =
O'
C =
O'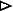 C = O.
C = O.
Thus, we have constructed O, the center of the circle passing through the three points P, Q, and R.
April, 1998
David E. Joyce
Department of Mathematics and Computer Science
Clark University
Worcester, MA 01610

My Homepage