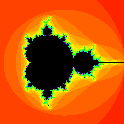
 The typical parameterization is in terms of a complex parameter µ, and the function being
iterated is f(z) = z2 - µ. If the set
The typical parameterization is in terms of a complex parameter µ, and the function being
iterated is f(z) = z2 - µ. If the set

This is part of the Introduction to Julia and Mandelbrot Sets. For more information on complex numbers, see Dave's Short Course on Complex Numbers.
 The typical parameterization is in terms of a complex parameter µ, and the function being
iterated is f(z) = z2 - µ. If the set
The typical parameterization is in terms of a complex parameter µ, and the function being
iterated is f(z) = z2 - µ. If the set
is bounded, then µ lies in the Mandelbrot set. With this parameterization, the most notable
feature of the set is a cardioid studded with circles.
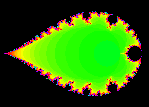 This isn't so much a different parameterization, but a different view of the usual parameterization.
If alpha = 1/µ, then the function being iterated is f(z) = z2 -
1/alpha. With respect to this parameterization, a point belongs to the Mandelbrot set in the
1/µ-plane if its inverse belongs to the Mandelbrot set in the µ-plane.
This isn't so much a different parameterization, but a different view of the usual parameterization.
If alpha = 1/µ, then the function being iterated is f(z) = z2 -
1/alpha. With respect to this parameterization, a point belongs to the Mandelbrot set in the
1/µ-plane if its inverse belongs to the Mandelbrot set in the µ-plane.
The inverse of the cardioid is the exterior of a teardrop shape. The circles on the outside of the
cardioid are inverted to circles on the inside of the teardrop. The cusp of the cardioid becomes the
cusp of the teardrop.
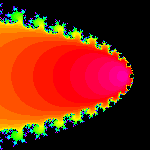 With this transformation, the cardioid is sent to the outside of a parabola. The circles on the
outside of the cardioid are inverted to circles on the inside of the parabola.
With this transformation, the cardioid is sent to the outside of a parabola. The circles on the
outside of the cardioid are inverted to circles on the inside of the parabola.
All three of these planes, the µ-plane, the 1/µ-plane, and the 1/(µ+.25)-plane are
planar representations of the same complex sphere. These transformations preserve the features of
inversive geometry. In particular, circles remain circles under inversive transformations.
is bounded, then lambda lies in the Mandelbrot set.
 The correspondence between µ and lambda is
µ = lambda2/4 - lambda/2.
Note that two values of lambda correspond to one value of µ, except that only one value of lambda
corresponds to the cusp of the cardioid in the µ-plane. In effect, the cardioid is doubled into
a pair of circles in the lambda-plane. The precise relation between lambda and µ is that lambda
is 1 plus or minus the square root of (1+4µ), and µ is 1/4 of lambda squared minus 2
lambda.
The correspondence between µ and lambda is
µ = lambda2/4 - lambda/2.
Note that two values of lambda correspond to one value of µ, except that only one value of lambda
corresponds to the cusp of the cardioid in the µ-plane. In effect, the cardioid is doubled into
a pair of circles in the lambda-plane. The precise relation between lambda and µ is that lambda
is 1 plus or minus the square root of (1+4µ), and µ is 1/4 of lambda squared minus 2
lambda.
Each circle has radius 1. The left circle is centered at lambda = 0 while the right circle is centered at lambda=2. They meet at lambda = 1, which corresponds to the cusp µ = -0.25 in the µ-plane.
One particularly nice aspect of the lambda-plane is that the circles are attached to the unit circle (the one centered at lambda=0) at the roots of unity. There is a big circle attached at 1, a smaller circle at -1, two smaller circles at the two primitive third roots of 1, two smaller circles at the two primitive fourth roots of 1, that is at i and -i, and so on.
 If the lambda-plane is inverted, everything outside the unit circle is moved inside the unit circle
and vice versa.
The left circle in the lambda-plane becomes the outside of the unit circle while the right circle
becomes a circle inside the unit circle attached at the point 1. This image also shows circles
attached at the roots of unity.
If the lambda-plane is inverted, everything outside the unit circle is moved inside the unit circle
and vice versa.
The left circle in the lambda-plane becomes the outside of the unit circle while the right circle
becomes a circle inside the unit circle attached at the point 1. This image also shows circles
attached at the roots of unity.
 Perhaps the most interesting presentation based on lambda is found by translating the lambda plane
left one unit then inverting. The point where the two circles meet is moved to zero, then inverted
off to infinity. The interiors of the two circles are mapped to the outside of an infinite vertical
strip. The strip is one unit wide centered at 0. Small circles are tangent to the sides of the strip
and inside the strip. Note that the circles are not of uniform size and they aren't uniformly
placed.
Perhaps the most interesting presentation based on lambda is found by translating the lambda plane
left one unit then inverting. The point where the two circles meet is moved to zero, then inverted
off to infinity. The interiors of the two circles are mapped to the outside of an infinite vertical
strip. The strip is one unit wide centered at 0. Small circles are tangent to the sides of the strip
and inside the strip. Note that the circles are not of uniform size and they aren't uniformly
placed.
 Inverting on that point makes all these circles larger and larger instead of smaller and smaller.
Exploring this inverted plane can be quite interesting. The original cardioid is turned around and
distorted a bit. It appears near the center of this image. The big circle to its left is the
inversion of the small circle to the right of the original cardioid. The little bit of a line moving
off to the right of the image is the end of the path in the µ-plane ending at z = 2.
Here's a big view of this plane, where x and y each vary from -400
to +400.
Inverting on that point makes all these circles larger and larger instead of smaller and smaller.
Exploring this inverted plane can be quite interesting. The original cardioid is turned around and
distorted a bit. It appears near the center of this image. The big circle to its left is the
inversion of the small circle to the right of the original cardioid. The little bit of a line moving
off to the right of the image is the end of the path in the µ-plane ending at z = 2.
Here's a big view of this plane, where x and y each vary from -400
to +400.
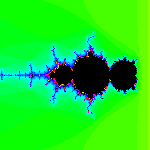 The end of the Mandelbrot set occurs at the point 2.0. We'll invert the µ-plane there
for this last version. The original cardioid looks smaller, and the first circle larger.
The finite line studded with cardioids that used to end at 2.0 now goes off to minus
infinity.
The end of the Mandelbrot set occurs at the point 2.0. We'll invert the µ-plane there
for this last version. The original cardioid looks smaller, and the first circle larger.
The finite line studded with cardioids that used to end at 2.0 now goes off to minus
infinity.
© 1994.

These pages are located at http://aleph0.clarku.edu/~djoyce/julia/