History of Trigonometry Outline

Trigonometry is, of course, a branch of geometry, but it differs from the synthetic geometry of Euclid and the ancient Greeks by being computational in nature. For instance, Proposition I.4 of the Elements is the angle-side-angle congruence theorem which states that a triangle is determined by any two angles and the side between them. That is, if you want to know the remaining angle and the remaining two sides, all you have to do is lay out the given side and the two angles at its ends, extend the other two sides until they meet, and you've got the triangle. No numerical computations involved.

But the trigonometrical version is different. If you have the measurements of the two angles and the length of the side between them, then the problem is to compute the remaining angle (which is easy, just subtract the sum of the two angles from two right angles) and the remaining two sides (which is difficult). The modern solution to the last computation is by means of the law of sines. Details are at Dave's Short Trig Course, Oblique Triangles.

All trigonometrical computations require measurement of angles and computation of some trigonometrical function. The modern trigonometrical functions are sine, cosine, tangent, and their reciprocals, but in ancient Greek trigonometry, the chord, a more intuitive function, was used.

Trigonometry, of course, depends on geometry. The law of cosines, for instance, follows from a proposition of synthetic geometry, namely propositions II.12 and II.13 of the Elements. And so, problems in trigonometry have required new developments in synthetic geometry. An example is Ptolemy's theorem which gives rules for the chords of the sum and difference of angles, which correspond to the sum and difference formulas for sines and cosines.

The prime application of trigonometry in past cultures, not just ancient Greek, is to astronomy. Computation of angles in the celestial sphere requires a different kind of geometry and trigonometry than that in the plane. The geometry of the sphere was called "spherics" and formed one part of the quadrivium of study. Various authors, including Euclid, wrote books on spherics. The current name for the subject is "elliptic geometry." Trigonometry apparently arose to solve problems posed in spherics rather than problems posed in plane geometry. Thus, spherical trigonometry is as old as plane trigonometry.

The Babylonians and angle measurement

The Babylonians, sometime before 300 B.C.E. were using degree measurement for angles. The Babylonian numerals were based on the number 60, so it may be conjectured that they took the unit measure to be what we call 60°, then divided that into 60 degrees. Perhaps 60° was taken as the unit because the chord of 60° equals the radius of the circle, see below about chords. Degree measurement was later adopted by Hipparchus.

The Babylonians were the first to give coordinates for stars. They used the ecliptic as their base circle in the celestial sphere, that is, the crystal sphere of stars. The sun travels the ecliptic, the planets travel near the ecliptic, the constellations of the zodiac are arranged around the ecliptic, and the north star, Polaris, is 90° from the ecliptic. The celestial sphere rotates around the axis through the north and south poles. The Babylonians measured the longitude in degrees counterclockwise from the vernal point as seen from the north pole, and they measured the latitude in degrees north or south from the ecliptic.

Hipparchus of Nicaea (ca. 180 - ca. 125 B.C.E.)

Hipparchus was primarily an astronomer, but the beginnings of trigonometry apparently began with him. Certainly the Babylonians, Egyptians, and earlier Greeks knew much astronomy before Hipparchus, and they also determined the positions of many stars on the celestial sphere before him, but it is Hipparchus to whom the first table of chords is attributed. It has been hypothesized that Apollonius and even Archimedes constructed tables of chords before him, but there is no reference to any such earlier table.

Some of Hipparchus' advances in astronomy include the calculation of the mean lunar month, estimates of the sized and distances of the sun and moon, variants on the epicyclic and eccentric models of planetary motion, a catalog of 850 stars (longitude and latitude relative to the ecliptic), and the discovery of the precession of the equinoxes and a measurement of that precession.

According to Theon, Hipparchus wrote a 12-book work on chords in a circle, since lost. That would be the first known work of trigonometry. Since the work no longer exists, most everything about it is speculation. But a few things are known from various mentions of it in other sources including another of his own. It included some lengths of chords corresponding to various arcs of circles, perhaps a table of chords. Besides these few scraps of information, others can be inferred from knowledge that was taken as well-known by his successors.

Chords as a basis of trigonometry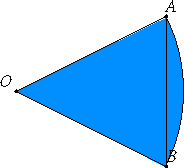

In a modern presentation of trigonometry, the sine and cosine of an angle a are the y- and x-coordinates of a point on the unit circle, the point being the intersection of the unit circle and one side of the angle a; the other side of the angle is the positive x-axis. The Greek, Indian, Arabic, and early Europeans used a circle of some other convenient radius. For this description of trigonometry, we'll leave the radius unspecified as r and it's double, the diameter, we'll denote d.

The chord of an angle AOB where O is the center of a circle and A and B are two points on the circle, is just the straight line AB. Chords are related to the modern sine and cosine by the formulas

crd a = d sin (a/2)

sin a = (1/d) crd 2a

    crd (180° - a) = d cos (a/2)

cos a = (1/d) crd (180° - 2a)

where a is an angle, d the diameter, and crd an abbreviation for chord.

Some properties of chords could not have escaped Hipparchus' notice, especially in a 12-book work on the subject. 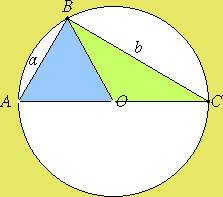For instance, a supplementary-angle formula would state that if AOB and BOC are supplementary angles, then Thales' theorem states that triangle ABC is right, so the Pythagorean theorem says the square on the chord AB plus the square on the chord BC equals the square on the diameter AC. Summarized using a modern algebraic notation

crd2 AOB + crd2 BOC = d2

where d is the diameter of the circle.

Hipparchus probably constructed his table of chords using a half-angle formula and the supplementary angle formula. The half-angle formula in terms of chords is

crd2(t/2) = r(2r - crd (180° - t)

where r is the radius of the circle and t is an angle. Starting with crd 60° = r, Hippocrates could by means of this half-angle formula find the chords of 30°, 15°, and 7 1/2°. He could complete a table of chords in 7 1/2° steps by using crd 90°, the half-angle formula, and the supplementary angle formula.

What other relations among the chords of various angles that Hippocrates would have known remains speculation.

Menelaus (ca. 100 C.E.)

The earliest work on spherical trigonometry was Menelaus' Spherica. It included what is now called Menelaus' theorem which relates arcs of great circles on spheres. Of course, Menelaus stated his result in terms of chords, but in terms of modern sines, his theorem reads

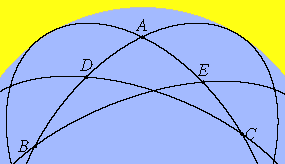
sin CE
sin EA		  =  sin CF
sin FD		   sin BD
sin BA
and
sin CA
sin EA		  =  sin CD
sin FD		   sin BF
sin BE


He proved this result by first proving the plane version, then "projecting" back to the sphere. The plane version says

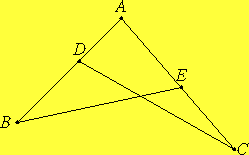
CE
EA		  =  CF
FD		   BD
BA
and
CA
EA		  =  CD
FD		   BF
BE


Ptolemy (ca. 100 - 178 C.E.)

Claudius Ptolemy's famous mathematical work was the Mathematike Syntaxis (Mathematical Collection) usually known as the Almagest. It is primarily a work on astronomy which included mathematical theory relevant to astronomy. It included trigonometric table, a table of chords for angles from 1/2° to 180° in increments of 1/2°, the chords were rounded to two sexagesimal places, about five digits of accuracy. He also included the geometry necessary to construct the table. He computed the chord of 72°, an central angle of a pentagon, a constructable angle. Along with the chord of 60° (the radius which Ptolemy took to be 60), that gives crd 12°, then crd 6°, crd 3°, crd 1 1/2°, and crd 3/4°. He used interpolation to find crd 1° and crd 1/2°.

Ptolemy's Theorem

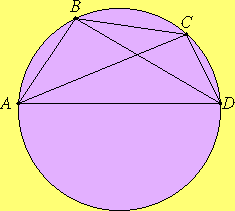Ptolemy proved the theorem that gives the sum and difference formulas for chords. When AD is a diameter of the circle, then the theorem says

crd AOC crd BOD = crd AOB crd COD + d crd BOC.

where O is the center of the circle and d the diameter. If we take a to be angle AOB and b to be angle AOC, then we have

crd b crd (180° - a) = crd a crd (180° - b) + d crd (b - a)

which gives the difference formula

crd (b - a) =  crd b crd (180° - a) - crd a crd (180° - b)
d

With a different interpretation of a and b, the sum formula results:

crd (b + a) =  crd b crd (180° - a) + crd a crd (180° - b)
d

These, of course, correspond to the sum and difference formulas for sines.

Armed with his theorem, Ptolemy could complete his table of chords from 1/2° to 180° in increments of 1/2°.

Trigonometry

Computational trigonometry could only begin after the construction of a good trig table, and so Ptolemy proceeded. Although he did not systematically give methods for solving right triangles and oblique triangles, solutions to specific problems are found in the Almagest. Those solutions that we would find using sines or cosines are equally easy to solve with a table of chords, but those that we would solve with tangents would require dividing a chord by the supplementary chord, making for a more difficult solution. A typical example of that would be finding the height of a pole given the length of its shadow and the angle of inclination of the shadow.

The primary source of information in this outline is Thomas Heath's A History of Greek Mathematics, Clarendon Press, Oxford, 1921, currently reprinted by Dover, New York, 1981.

David E. Joyce,