Math 120 Calculus IFall 2014 Prof. D. Joyce, BP 322, 793-7421 Department of Mathematics and Computer Science Clark University |
Math 120 Calculus IFall 2014 Prof. D. Joyce, BP 322, 793-7421 Department of Mathematics and Computer Science Clark University |
Calculus is essential for majors in biology, chemistry, computer science, mathematics, physics, and environmental science and policy. Part I includes functions, limits, continuity, differentiation of algebraic and trigonometric functions, mean value theorem, and various applications. Part II includes Riemann sums and integrals, techniques and applications of integration, improper integrals, transcendental functions (logarithms, exponential functions, and inverse trigonometric functions), sequences, and series. Though not all results are derived rigorously, care is taken to distinguish intuitive arguments from rigorous proofs. Math 120 and 121 each fulfill the Formal Analysis requirement.
Prerequisite for Math 120: appropriate score on the mathematics placement test, or appropriate grade in Math 119. Prerequisite for Math 121: Math 120, or Math 124, or AP credit in Calculus. Offered every fall (120) and spring (121).
See also Clark University Academic Catalog for information on the Honors Calculus sequence (Math 124 and 125).
This first semester, Math 120, includes differential calculus, the concept of integration, and the Fundamental Theorem of Calculus (FTC) which connects differentiation to integration. Topics include functions, limits, continuity, differentiation of algebraic and trigonometric functions, mean value theorem, applications of derivatives, definition of integrals and their basic properties, and the FTC.
Next semester, Math 121, covers techniques of integration, applications of integration, a short introduction to differential equations, sequences, series, and power series.

We will discuss the first four chapters and part of the fifth chapter in Math 120. This same book will also be used in Math 121.
Accessing MyMathLab. To register for MyMathLab course online, you will need:
To get precise registration instructions, go to MyMathLab, http://pearsonmylabandmastering.com, and, on the right, click on Student under Register. There you will give your course ID and follow the steps given. Be careful to put in your name precisely as it appears in the university records.
At the end of the registration process you will have a login name and password. Each time you want to access MyMathLab, click on Sign in (under sign in, and then put in your data. On the left of the resulting screen you will see Math 120-.... Click on that.
On the web page that comes up you’ll see buttons on the left that are used to give the various options of the software. From here you can do an assignment, take a test, etc. There’s a button Study Plan, which allows you to practice problem solving, with help from the program if requested. You also have a Multimedia Library which contains useful material.
By the way, you can access MyMathLab from any computer on the internet. There are computers in Goddard Library if you don’t have one or if yours breaks down.
As a final note, remember that aside from online support, Pearson offers tech support for MyMathLab, so you can call them if anything goes wrong. The Pearson 24/7 Technical Support web page is at http://247pearsoned.custhelp.com/. (In the past the web site has sometimes been down for short periods of time, but it came back up fairly quickly.)
The course will use the software MyMathLab for the homework assignments. It will also be employed to practice problem solving. To start using it, you must register to your section online at http://pearsonmylabandmastering.com/ using the Course ID given to you by your instructor and your access code.
If you get an exercise wrong, you'll be able to try it a second time. If you’re ill or otherwise need an extension, that can be arranged. Otherwise, late exercises will by reduced by 25%, and they'll only be available for a few days after the due date.
The assignments are all on line, but if for any reason you can’t access them, here’s a corresponding list of exercises from the text. They’ll be assigned as the course progresses.
Some of the questions on the assignments will ask you for numerical answers. A standard scientific calculator has everything you need. The one on a computer if sufficient for that.

Preview. Calculus is about the relation between a quantity and its rate of change. For an example, if the quantity is the distance (from the initial position) on a line at a given time, then its rate of change is velocity. If the velocity is constant, then calculus is not required: the distance travelled is the product of the elapsed time and the velocity. But when the velocity is not constant, then this formula doesn’t apply. Nonetheless, the distance and velocity are intimately related. If the distance at all times is known, then the velocity at any given time can be determined; and if the velocity at all times is known, then the distance at any given time can be determined. These two operations are called differentiation and integration.
Much of calculus involves analyzing and developing these concepts and their applications.
Proofs are going to used throughout the course. When we first meet a concept, we’ll discuss it intuitively. Then we’ll formalize it with a formal definition. We’ll use that definition to prove the things we expect to be true actually are true.
Notes:
Chapter 1. Review of functions. There are a slew of things in the first chapter that you should already know. We aren’t going to cover them in class. We’ll mention a couple of them, but chapter 1 is primarily there to show you some of the things that you’re supposed to know already.
Besides what’s in chapter 1, there are all the things on the page Mathematics background needed for calculus at http://aleph0.clarku.edu/~djoyce/ma120/background.html too.
If you’re trigonometry is rusty, you can look at Dave's short course in Trig for a review of trigonometry.
Chapter 2. Limits and Continuity. After the introduction explaining where we’re going, this is where the subject matter starts.
We first must clarify the concept of derivative. In some ways it is intuitively clear that a travelling body has a velocity, or more generally, any changing quantity has a rate of change. But just what is the rate of change? The answer is that the rate of change at an instant is the limit of the average rates of change near that instant. That is, the derivative (instantaneous rate of change) of a function f(x) is the limit of the average rate of change of the function over an interval [x, x+h] as the length h of that interval approaches 0. The average rate of change over the interval is how much f(x) changes over that interval divided by the length of the interval h. We want the limit of that average as the length h approaches 0.
The concept of limit is much more subtle than it first appears. We will discuss it in some detail and develop a formal defintion of a limit and a formal notation to go along with it.
Key concepts associated to the concept of limit are tangent lines, limit laws, continuity, the sandwich theorem (also known as the pinching theorem), the formal definition for limits, discontinuities, asymptotes, continuity, the intermediate value theorem (IVT), and the definition of a derivative (which is why we study limits in the first place).
Notes:
Chapter 2 Limits and Continuity
Chapter 3. Derivatives. Now that we’ve got a solid definition of limit (that was section 2.7), we can start to study derivatives. There are a number of rules for differentiation (finding derivatives), mostly easily learned, although the chain rule, for some reason, seems to be more difficult to master. There are a couple of different notations for derivatives that everyone uses.
It is assumed that you know the trig functions, sine, cosine, etc., and we will find and use their derivatives. Further topics in differentiation include higher derivatives, implicit differentiation, differentiation of inverse functions, and differentiation of logarithms. We’ll finish this chapter studying situations when several quantities are changing; we’ll see how their derivatives are related.
Notes:
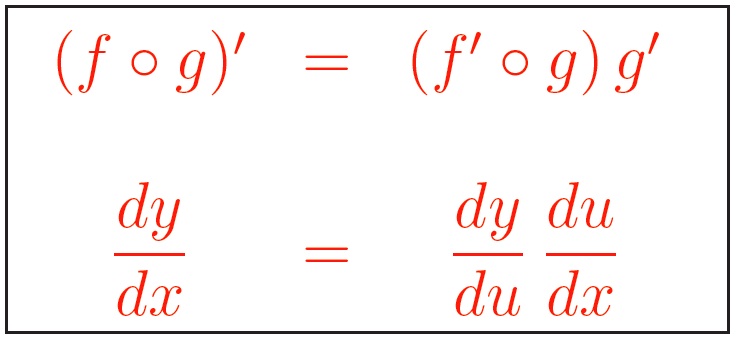
Chapter 3 Differentiation
Chapter 4. The Mean Value Theorem and Applications. We’ll verify some intuitive ideas with formal proofs. For instance, if the derivative is positive, then the function is increasing; at a maximum or a minimum of a function, the derivative is zero. We will prove these (obvious) statements using a theorem called the mean value theorem. We’ll also do some curve sketching. The purpose of curve sketching is no so much to draw the graph of the function, but to get a better understanding of the relation between a function and its derivative. We’ll also see what second derivatives have to do with the graph of a function.
The applications of derivatives are numerous. Besides classical applications in physics and the natural sciences, there are applications in the social sciences, for instance, marginal profits are just derivatives of profits.
 Notes:
Notes:
Chapter 4. The Mean-Value Theorem and applications
Chapter 5. Integration and the Fundamental Theorem of Calculus (FTC). Derivatives are only half of calculus. We studied them first because they’re the easier half. The other half is integration. For a positive function, its integral is just the area under the graph of the function. Although for many purposes, the intuitive concept of area is enough to understand and use integrals, we’ll look at a more formal algebraic definition in terms of limits. It gives a way of approaching that area that can be used in practice and in theoretical proofs. We’ll close with a formal proof of the FTC which ties together the main topics of the course.
Notes:
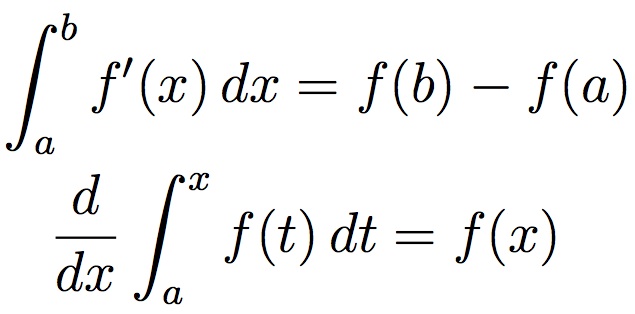
Chapter 5 Integration and the FTC
Besides the time for classes, you’ll spend time on reading the text, doing the assignments, and studying of for quizzes and tests. That comes to about five to nine hours outside of class on average per week, the actual amount varying from week to week. For more detail about how to study mathematics, see About studying mathematics in general, and Calculus in particular.
Dates for the midterms and finals are to be determined. The first test will be about 1/3 of the way through the semester, the second about 2/3.
Class attendance and class participation are obligatory. During the class meetings the text will be supplemented with more rigorous theory and special topics. Turn off your cell phones during class. Laptops may only be used for class-related purposes—no texting, no browsing, no email.
Calculators, cell phones, and laptops may not be used during tests.

This page is located on the web at
http://aleph0.clarku.edu/~djoyce/ma120/
David E. Joyce
