

A horocycle (or limiting curve)can be created as follows: start with a line l point Q on l and erect a perpendicular line PQ to l through Q. Then consider the circle symbolized by delta with center P and radius PQ, which is tangent to l at Q. If P were to move further from l along the perpendicular line, then the circle, delta, would increase in size and remain tangent to l. As P moves arbitrarily futher from Q, delta will eventually approarch a limiting position. In Euclidean geometry the limiting position of delta would be the line l; however, in hyperbolic geometry the limiting position of delta is a new curve h called a limiting curve or horocycle.
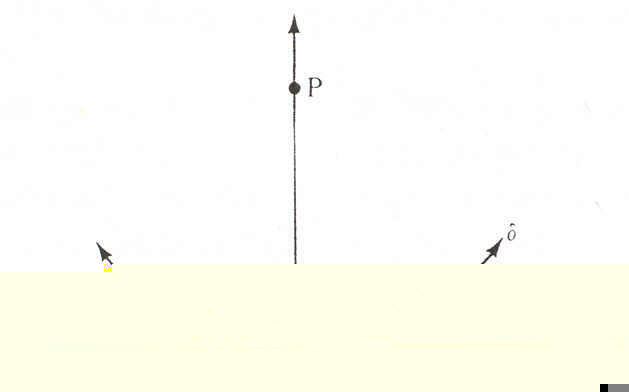
This can be visualized in the Poincare model as follows: let l be a diameter of the Euclidean circle y whose interior represents the hyperbolic plane, and let Q be the center of y.
As P moves away from Q towards the ideal point represented by S, R is pulled up to the Euclidean midpoint of SQ, so the horocycle h is a Euclidea circle tangent to y at S and tangent to l at Q.
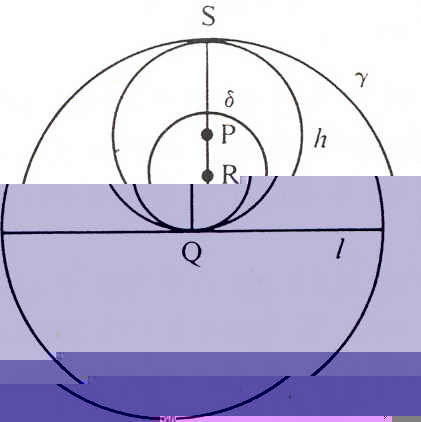
In general, horocycles are represented in the Poincare model by Euclidean circles inside y and tangent to y.
Two horocycles tangent to y are called concentric.
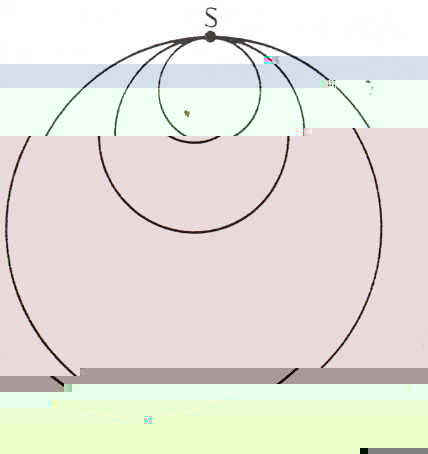
A horocycle is the curve traced out by the pointin the hyperbolic plane that is subjetced to a parabolic transformation. Parabolic transformations have one fixed point p on the unit circle. The transformation is called a parallel displacement, and, under its influence, points move into the unit disk away from the ideal point p and then back out to p.
