Wouldn't it be nice to see why all these dry parts of synthetic geometry are there? Why they can't be skipped so that you can go directly to the good parts? Well, let's do that!

Let's start with the good parts and work our way backward. The standard presentation has three stages: (1) axioms and definitions, (2) basic theorems, (3) interesting theorems. But the standard presentation is the eventual product of a process, not the way it began. The process began with interesting propositions and a search to figure out why they're true. The answer to why they're true became the synthetic geometry in its standard presentation.

So what we'll do is to try to figure out why the interesting theorems are true. That's called an analysis of geometry. Analysis means we'll break things down into their parts. The result of this analysis of geometry will be the synthetic geometry.

Let's take one interesting result in geometry, one that's not too complicated, and analyze it. Let's take the Pythagorean theorem. It's a very important theorem, it's an interesting theorem, and it's surprising in the sense that you wouldn't guess it if you didn't already know it. (That leads to an interesting historical question: how did anybody ever discover it in the first place?)

The Pythagorean Theorem.

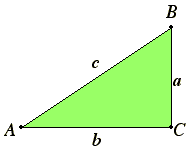
First, what is it? The statement of the theorem, as we usually see it now, is that given a right triangle, the square of the hypotenuse is the sum of the squares of the other two sides. We're used to seeing this as an algebraic equation. If the hypotenuse has length c, while the lengths of the other two sides are a and b, then

Why is it called the Pythagorean theorem? It was thought that Pythagoras of Samos (born about 570 B.C.E, died about 490 B.C.E), or one of the later Pythagoreans who followed him, proved it. The Pythagoreans certainly knew it was true, and that was about the time that proofs became important to geometers, so it could well be that the Pythagoreans had a proof. But then again, we don't have much evidence, so perhaps it wasn't proved until a bit later, sometime before Euclid (about 300 B.C.E.). In any case, we should make the distinction between knowing something is true and knowing why it is true. I'll try to use the word "theorem" to mean a statement that has a proof, and "rule" for a statement known, or believed, to be true, but perhaps without a proof. So, the Pythagoreans who knew it at least accepted the Pythagorean rule, and once they had proved it (if they in fact did prove it) had the Pythagorean theorem.

This Pythagorean rule was known in many other cultures, some long before Pythagoras. The earliest people who we can document knew the Pythagorean rule were the Babylonians, who at least as early as 1800 B.C.E. were using the Pythagorean rule. That's about a millenium and an half before Pythagoras. In light of that, we should probably use a different name. I would suggest "rule of the right triangle," but Pythagoras' name is so much attached to this theorem, or rule, that it's probably futile to try to change the name.

Why is it true? Our job it to figure out why the Pythagorean rule is true. In other words, we're looking for a proof. At this point, we don't need a completely formal proof of it. After all, we'll be developing a theory of plane geometry so that we can completely formally prove it. Right now, all we need is a convincing argument for the Pythagorean rule.

There are many such arguments. Your job is to find one. You can use any argument except Euclid's. Euclid has a formal proof in Proposition 47 of Book I of the Elements. Since we'll be looking at that later to see how Euclid solved the problem of developing a theory of plane geometry, let's not consider it now.

Your assignment. So, either on your own, or with others, or by looking it up, find a proof of the Pythagorean rule. It's pretty hard to come up with a proof yourself, especially if you've never seen any proof of it, but it's fun to try, and you might succeed. You've probably seen one or more proofs before, and that should make it possible to develop one, even if you don't exactly remember what you saw. But you're welcome to look one up. Write up a brief summary of the proof you choose (any one except Euclid's).

We'll look at the various methods of proof in class and choose one or two of them to pursue as a class. We'll study this proof to see what assumptions it makes. Over the next few meetings, we'll analyze some of these assumptions further, and we'll turn those assumptions into other theorems with their own proofs. A few of them will be interesting theorems, but as we progress, the theorems will become more and more basic, less and less interesting, and more difficult to find more basic statement to base the proofs on. Those assumptions we don't find proofs for will become the axioms of our theory.

Back to course page

http://aleph0.clarku.edu/~djoyce/ma128/pyth.html