| Pierre-Simon Laplace (1749–1827) |
|---|
| |
|
|
 Portrait of Laplace at the Palace of Versailles
Portrait of Laplace at the Palace of Versailles
Date 1842, posthumous portrait by Sophie Feytaud
|
[This course page is obsolete. I'll update it next time I teach the course.]
Please bookmark this page, http://aleph0.clarku.edu/~djoyce/ma217/, so you can readily access it.
Course information
- General description.
An introduction to probability theory and mathematical statistics that emphasizes the
probabilistic foundations required to understand probability models and statistical
methods. Topics covered will include the probability axioms, basic combinatorics,
discrete and continuous random variables, probability distributions, mathematical
expectation,
common families of probability distributions, and the central limit theorem.
This course is cross-listed as Econ 360.
See also
Clark’s Academic Catalog
- Prerequisites.
Math 130 Linear Algebra, and Math 131 Multivariate Calculus

- Course goals.
- To provide students with a good understanding of the theory of probability, both
discrete and continuous, including some combinatorics, a variety of useful
distributions, expectation and variance, analysis of sample statistics, and
central limit theorems, as described in the syllabus.
- To help students develop the ability to solve problems using probability.
- To introduce students to some of the basic methods of statistics and prepare them
for further study in statistics.
- To develop abstract and critical reasoning by studying logical proofs and the
axiomatic method as applied to basic probability.
- To make connections between probability and other branches of mathematics, and
to see some of the history of probability.
- Syllabus
- Basic combinatorics. Additive and multiplicative principles, permutations,
combinations, binomial coefficients and Pascal’s triangle, multinomial coefficients
- Kolmogorov’s axioms of probability. Events, outcomes, sample spaces, basic
properties of probability. Finite uniform probabilities. Philosophies of
probability.
- Conditional probability. Bayes’ formula, independent events, Markov chains
- Random variables. Discrete random variables/distributions, expectation, variance,
Bernoulli and binomial distributions, geometric distribution, negative binomial
distribution, expectation of a sum, cumulative distribution functions
- Continuous random variables. Their expectation and variance. Uniform continuous
distributions, normal distributions, Poisson processes, exponential distributions;
gamma, Weibull, Cauchy, and beta distributions

- Joint random variables. Their distributions, independent random variables, and
their sums. Conditional distributions both discrete and continuous, order
statistics
- Expectation. Of sums, sample mean, of various distributions, moments, covariance
and correlation, conditional expectation
- Limit theorems. Chebyshev’s inequality, law of large numbers, central limit
theorem
- Textbook. A First Course in Probability, 9th edition, by Sheldon Ross.
Pearson, 2014.
We may occasionally also refer to an on-line textbook,
Charles M. Grinstead and J. Laurie Snell’s Introduction to
Probability, published by the American Mathematical Society, 1997, on-line at
http://www.dartmouth.edu/~chance/teaching_aids/books_articles/probability_book/book.html
..
- Course Hours. MWF 9:00–9:50.
- Assignments & tests.
There will be numerous short homework assignments, mostly
from the text, occasional quizzes, two tests during the semester, and a two-hour
final exam during finals week.
- Time and study.
Besides the time for classes, you’ll spend time on reading the text, doing the
assignments, and studying of for quizzes and tests. That comes to about five to nine
hours outside of class on average per week, the actual amount varying from week to
week.
- Course grade. [tentative]
The course grade will be determined as follows:
2/9 assignments and quizzes,
2/9 each of the two midterms, and
1/3 for the final exam.
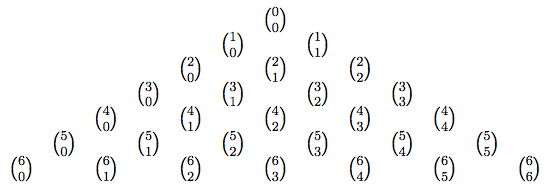 Class notes, quizzes, tests, homework assignments
Class notes, quizzes, tests, homework assignments
The dates for the discussion topics and the assignments are tentative. They will change as the course progresses.
- Monday, Aug 25. Welcome and introduction to the class
Intro to probability via discrete uniform probabilities. Symmetry. Frequency.
Simulations and random walks
- Wednesday, Aug 27.
Background on sets. Unions, intersections, complements, distributivity,
DeMorgan's laws. Product, power sets. Countable and uncountable infinities.
Combinatorics. Principle of inclusion and exclusion, multiplicative principle, permutations, factorials and Sterling's approximation
Permutation generating applet
Assignment 1 due next Wednesday.
- Friday, Aug 29. Binomial coefficients.
Combinations, Pascal's triangle, multinomial coefficients, stars & bars, combinatorial proofs

The BinomialPlot and
GaltonBoard applets
Monday, Sep 1. Labor Day. No classes
- Wednesday, Sep 3. Axioms for probability distributions.
Probability mass mass functions for discrete distributions, density functions for continuous
distributions. Cumulative distribution functions. Sample spaces, axioms, and properties.
Assignment 1 due.
Assignment 2 due next Wednesday.
- Friday, Sep 5. Uniform finite probabilities
Odds. Repeated trials. Sampling with replacement. The birthday problem.
The Birthday applet
- Monday, Sep 8. Proofs of properties of probability distributions from the axioms.
Conditional probability. Xox.
- Wednesday, Sep 10.
More on conditional probability: definition of conditional probability, the multiplication rule
Assignment 2 due.
Assignment 3 due next Wednesday.
- Friday, Sep 12.
Bayes' formula. Examples, tree diagrams
- Monday, Sep 15.
Independent events. Definition, product spaces, independence
of more than two events, joint random variables, random samples, i.i.d. random variables
Bertrand's box paradox
- Wednesday, Sep 17.
The Bernoulli process. Sampling with replacement. Binomial
distribution, geometric distribution, negative binomial distribution, hypergeometric
distribution. Sampling without replacement
Assignment 3 due.
Assignment 4 due next Wednesday.
- Friday, Sep 19.
Discrete random variables. Probability mass functions, cumulative
distribution functions. Various graphs and charts
Expectation for discrete random variables. Definition,
expectation for the binomial and geometric distributions. St. Petersburg paradox.
- Monday, Sep 22.
Select the date for the first test. It will cover chapter 1 through most of chapter 4.
More on expectation. Properties of expectation.
Variance for discrete random variables. Definition and properties.
- Wednesday, Sep 24.
Variance of the binomial and geometric distributions.
Assignment 4 due.
Assignment 5 due next Wednesday.
- Friday, Sep 26.
Continuous probability. Monte Carlo estimates. Introduction to
the Poisson process and the normal distribution. Statement of the central limit theorem.
- Monday, Sep 29.
Density functions. Density as the derivative of the c.d.f., and
the c.d.f. as the integral of density.
- Wednesday, Oct 1.
Assignment 5 due.
- Friday, Oct 3.
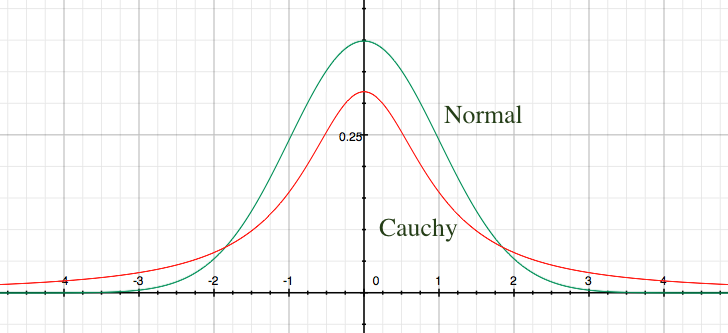
Examples of continuous distributions, functions of random variables, the Cauchy distribution.
- Monday, Oct 6. Review for first test
Sample first test
- Wednesday, Oct 8.
First test. Covers chapter 1 through 4.
Answers. Extra answers.
- Friday, Oct 10.
The Poisson process. The Poisson, exponential, gamma, and
beta distributions. Axioms for the Poisson process.
Monday, Oct 13. Fall break. No classes.
- Wednesday, Oct 15.
Expectation and variance for continuous random variables.
Definitions and properties. Expectation and variance for uniform and continuous distributions.
Lack of expectation and variance for the Cauchy distribution.
Assignment 6 due next Wednesday.
- Friday, Oct 17. The normal distribution, table for the c.d.f. of the standard normal distribution,
the normal approximation to the binomial distribution. DeMoivre's 1733 proof for the first instance
of the Central Limit Theorem.
- Monday, Oct 20.
Joint distributions. Independent random variables. Joint c.d.f.'s and joint density functions.
- Wednesday, Oct 22. Partial derivatives and multiple integrals relating to joint distributions.
Assignment 6 due.
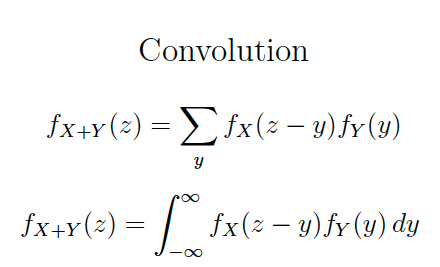
- Friday, Oct 24.
Sums and convolution. The discrete case.
Assignment 7 due next Wednesday.
- Monday, Oct 27. More on convolution. The continuous case.
Gamma distributions as convolution of exponential distributions.
Normal distributions convolute to other normal distributions.
- Wednesday, Oct 29.
Conditional distributions. Conditional cumulative distribution functions,
conditional probability mass functions, conditional probability density functions
Assignment 7 due.
- Friday, Oct 31.
Covariance and correlation.
Connection of covariance and variance, properties of covariance including bilinearity.
See Spurious Correlations to see that correlations often occur without associated causation.
- Monday, Nov 3.
Order statistics
- Wednesday, Nov 5. Review for second test
Sample second test
- Friday, Nov 7. Second test. On 4.7, 5, and 6.1–6.5 (through conditional distributions).
Answers. Extra answers.
- Monday, Nov 10.
Moments and the moment generating function
- Wednesday, Nov 12. Properties and examples of the moment generating function.
- Friday, Nov 14. Joint probability distributions of multivariate functions, the Jacobian.
Notes from multivariate calculus about the Jacobians
Assignment 8 due next Wednesday.
- Monday, Nov 17.
A proof of the central limit theorem
- Wednesday, Nov 19. Discussion of statistical inference.
Assignment 8 due. Answers
- Friday, Nov 21.
Bayesian statistics Part I: an example, the basic principle, the Bernoulli process
- Monday, Nov 24. Maximum likelihood estimators
Old notes from 218: Discrete case and
Continuous case
- Monday, Dec 1.
Bayesian statistics Part II: Bayes pool table, conjugate priors for the Bernoulli
process, point estimators, interval estimators
- Wednesday, Dec 3.
Bayesian statistics Part III: the Poisson process & its conjugate priors
Bayesian statistics Part IV: the normal distribution with known variance
- Friday, Dec 5.
Bayesian statistics Part V: the normal distribution with unknown variance
- Monday, Dec 8. Review.
Final will cover chapters 1–8 except sections 6.8, 7.6, 7.8, 7.9, 8.2, 8.4, 8.5.
Also there will be an essay question on Bayesian statistics.
Sample final exam
- Final exam.
Dec 16. 10:30. JC 220. Alternate Dec 12. morning, meet at my office sometime between 9 and noon.
Other information.
This page is located on the web at http://aleph0.clarku.edu/~djoyce/ma217/
David E. Joyce
 Portrait of Laplace at the Palace of Versailles
Portrait of Laplace at the Palace of Versailles

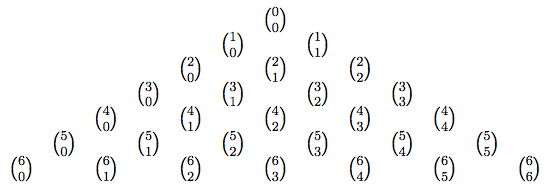 Class notes, quizzes, tests, homework assignments
Class notes, quizzes, tests, homework assignments

