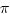 s, and
s, and
y = r sin 2
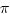 s,
s,Answer: The central Millefiori algorithm splatters a square with colored pixels iteratively. One point is chosen at random, then the next is computed from its coordinates. Think of the coordinates of the square as varying from 0 to 1, both the x- and the y-coordinates. So it's a unit square. If the old point is at (x,y) then the new point is computed as in this Pascal code
{compute the next point}
x := x + (y-k*x) * delta_t ;
if x >= 0.0 then
x := x - trunc (x)
else
x := x - trunc (x) + 1.0 ;
y := y - (x+k*y) * delta_t ;
if y >= 0.0 then
y := y - trunc (y)
else
y := y - trunc (y) + 1.0 ;
Here, the variables k and delta_t are parameters which adjust
how far away the point moves. If delta_t is very near 0, you get a
solid curve, a quarter circle. If delta_t lies between 0.05 and 1.95
interesting patterns result. The variable k is a second order
adjustment. When k is 0, then the patterns produced are a collection
of ovals, when k is slightly positive, like 0.001,
then the ovals turn into spirals growing in toward a center. When k is
slightly negative, then the ovals turn into spirals spiraling outwards.
Question 2: What's with the flowers?
Answer: I like flowers.
Question 2.1: I meant, how do you make the flowers?
Answer: Start with a square that's got a Millefiori! pattern in it. Each petal on the flower will be formed out of two of these squares, each twisted, then patched together. So if the flower has five petals, there will be ten twisted squares patched together to make the flower.
Now, each half-petal is shaped like a piece of pie with a curvy edge. The square will be mapped to the piece by sending one whole edge of the square to the corner of the piece, the two adjacent sides of the square to the to straight sides of the piece, and the remaining side of the square will be mapped to the curvy edge. This is actually done using polar coordinates.
Suppose the points in the square have coordinates (r,s) where 0 < r < 1 and 0 < s < 1. If we just set
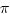 s, and
s, and
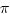 s,
s,We don't want the unit circle, but just a piece of it, in particular, 1/2n of it, where n is the number of petals on the flower. That's easily taken care of by adjusted the angle s in the equations:
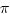 s/n, and
s/n, and
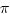 s/n.
s/n.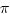 s/n, and
s/n, and
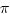 s/n.
s/n.Question 2.2: Okay, I'll bite. What function do you choose?
Answer: If you get the "Flowered Millefiori with parameters" form, you can specify six numerical parameters, namely, a, b, a', b', a'', and b''. These six parameters determine what the function f will be. This function f actually will be the unique fifth degree polynomial such that