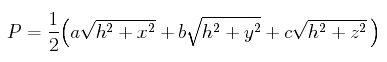
To begin analyzing the situation, draw lines DE, DF, and DG from D perpendicular to the sides a, b, and c of the triangle, with lengths x, y, and z, respectively. Also, draw lines from D to the vertices of the triangle.
Note that the lengths of x, y, and z cannot be freely chosen since any two determine the third. The first problem is to find an equation that relates them. The triangle ABC is composed of the three triangles BCD, ACD, and ABD. Those three triangles have areas ax/2, by/2, and cz/2, respectively. Therefore, the area T of triangle ABC is
Since the area T is a fixed quantity, this equation is the constraint that relates the variables x, y, and z.
The pyramid. Next, we can find a formula for the surface area of the pyramid. We're only concerned with the lateral area made up of the three side triangles since the base triangle is fixed. The side triangle on the line a has an altitude which is the square root of h2 + x2, so its area is that times a/2. The areas of the other two side triangles have analogous formulas, so the lateral surface area P of the pyramid is given by the formula
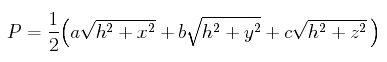
Now, what we have to do is maximize this quantity subject to the constraint on x, y, and z mentioned above.
Langrange multipliers. If we didn't have the constraint on the variables, then we could use basic calculus to find the solution. All we would have to do is take the three partial derivatives with respect to x, y, and z, set them all to 0, and simultaneously solve the resulting three equations to find the critical points where the extreme values of the function occur.
But we do have that constraint. Fortunately, the method of Lagrange multipliers applies in just this case. Introduce a new variable, let's call it w, and form a function of the four variables x, y,z, and w by taking the formula for the function we want to maximize and subtracting w times the constraint, after we rewrite the constraint as a function that has to be 0. That gives us the function
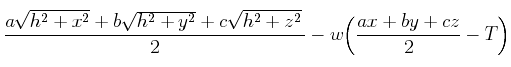
For the method of Lagrange multipliers, take the three partial derivatives with respect to x, y, and z, set them all to 0, and simultaneously solve the resulting three equations along with the constraint equation to find the critical points where the extreme values of the function occur.
The three partial derivatives set to 0 give the equations
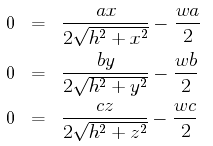
These three equations can be easily solved to give the unique solution x = y = z.
The incenter of the triangle. We conclude that the point D below the apex of the pyramid with the largest surface area is a point equidistant from the three sides of the triangle. It is called the incenter of the triangle. The distance r from the incenter to any side is called the inradius of the triangle.
For more information about the incenter, see Euclid's Elements, proposition IV.4 in which the incircle of a triangle is constructed as the intersection of any two angle bisectors of the triangle. (The incenter is not the only "center" of a triangle. See also the note about the Euler line of a triangle for some other triangle centers.)
Note that the area T of the triangle is the product of the radius r of the inradius and the semiperimeter s, which is (a + b + c)/2. So T = rs. The commentary to proposition IV.4 mentioned above also gives a derivation of Heron's formula for the area T of the triangle in terms of the semiperimeter s,and the sides a, b, and c, namely, T equals the square root of s(s – a)(s – b)(s – c).
Back to the minimal-area pyramid. We can now compute the lateral surface area of the minimal-area pyramid. It is
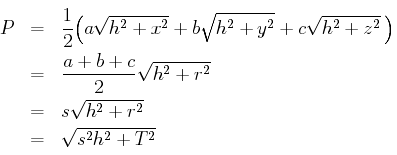
Back to Clark's Math Problem Solving Team page
This page is located at http://aleph0.clarku.edu/~djoyce/mpst/pyramid/
David E. Joyce, Oct. 2003
Department of Mathematics and Computer Science
Clark University
Worcester, MA 01610