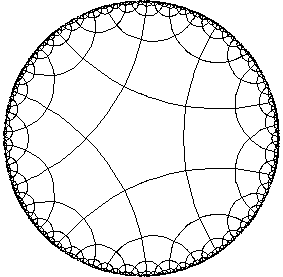

The selection of available tilings is shown in the following table. The row indicates n, the number of sides on a polygon, while the columin indicates k, athe number of polygons that meet at each vertex.

Some entries in the table are colored. They indicate tilings that are not hyperbolic. There are five elliptic tilings that correspond to the five regular solids. They are: the tetrahedron {3,3}, the octahedron {3,4}, the icosahedron {3,5}, the cube {4,3}, and the dodecahedron {5,3}. There are also three parabolic tilings, which are tilings of the ordinary Euclidean plane. They are {3,6} (tiling by equilateral triangles}, {4,4} (tiling by squares), and {6,3} (tiling by hexagons).
| Regular tilings | ||||||||
|---|---|---|---|---|---|---|---|---|
| 3 | 4 | 5 | 6 | 7 | 8 | 10 | 12 | |
| 3 | {3,7} | {3,8} | {3,10} | {3,12} | ||||
| 4 | {4,5} | {4,6} | {4,7} | {4,8} | {4,10} | |||
| 5 | {5,4} | {5,5} | {5,6} | |||||
| 6 | {6,4} | {6,5} | {6,6} | |||||
| 7 | {7,3} | {7,4} | {7,7} | |||||
| 8 | {8,3} | {8,4} | ||||||
| 10 | {10,3} | {10,4} | ||||||
| 12 | {12,3} | |||||||
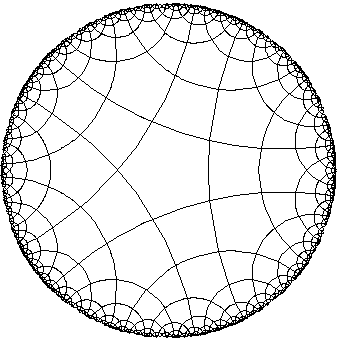
Quasiregular tilings. There are also a few quasiregular tilings available. They're listed in the table below. The quasiregular tiling {n|k} is made out of n-gons and k-gons. Each n-gon is bounded by k-gons, and each k-gon is bounded by n-gons. Two n-gons and two k-gons alternate around each vertex.
Note that the quasiregular tilings {n|k} and {k|n} are actually the same tiling of the hyperbolic plane. They appear different because a n-gon is placed in the center of the Poincaré disk for the first tiling, but a k-gon is placed in the center for the second tiling.
A quasiregular tiling {n|n} is the same as the regular tiling {n,4}, and so the diagonal entries in the table below refer to tilings mentioned in the first table.
| Quasiegular tilings | ||||||||
|---|---|---|---|---|---|---|---|---|
| 3 | 4 | 5 | 6 | 7 | 8 | 10 | 12 | |
| 3 | {3|7} | {3|8} | {3|10} | {3|12} | ||||
| 4 | {4|5} | {4|6} | ||||||
| 5 | {5|4} | {5|5} | {5|6} | |||||
| 6 | {6|4} | {6|5} | {6|6} | |||||
| 7 | {7|3} | {7|7} | ||||||
| 8 | {8|3} | {8|8} | ||||||
| 10 | {10|3} | {10|10} | ||||||
| 12 | {12|3} | |||||||
Create your own black & white tilings.
Dec 2002
David E. Joyce

Department of Mathematics and Computer Science
Clark University
Worcester, MA 01610
The address of this file is http://aleph0.clarku.edu/~djoyce/poincare/poincare.html