The Little Gallery of Roulettes
David E. Joyce

Clark University
Back in 1983 I wrote a bunch of programs to produce roulettes on the Tektronix
4105 terminal. Rather than forget them entirely, I've captured a few of the
resulting figures for this educational gallery of roulettes.
Roulettes are produced when circles revolve around or inside other circles.
More precisely, they are the locus of a point on, inside, or outside the
revolving circle. When the drawing point is right on the rotating circle, an
epicycloid or hypercycloid is produced.
Epicycloids
An epicycloid (Du¨rer 1525) is the locus of a point on the
circumference of which is rolling around the outside of a fixed circle. The
rolling circle does not have to have the same radius as the fixed circle, if
it does, then the resulting figure is heart shaped, and it's called a
cardioid.
(Although the cardioid is just a curve, it's interior is displayed because
that's nicer to look at than just the curve.)
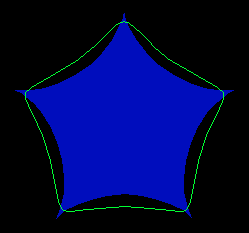
Here are some other epicycloids. The ratios of the radii of the fixed
circle to the rolling circle are 2:1 , 3:1, 4:1, and 5:1, respectively. The
2:1 epicycloid is also known as the nephroid and was studied by
Huygens, Tschirnhausen, and Bernoulli 1678-1692.
The radius of the fixed circle doesn't have to be a multiple of the
radius of the rolling circle; as long as this ratio is a rational number, the
resulting curve is closed. For instance, here are epicycloids with ratios of
1:2, 1:3, 2:3, and 3:2, respectively.
Some more epicycloids
with ratios of 16:7, 7:16, 16:21, and 21:16.
Hypocycloids
A hypocycloid is the locus of a point on the circumference of which
is rolling around the inside of a fixed circle. The rolling circle better not
have to have the same radius as the fixed circle, because if it did, then the
resulting figure would just be a point. Here are some hypocycloids with
ratios of 3:1, 4:1, 5:2, and 6:1, respectively. The 4:1 hypocycloid is
known as an astroid or tetracuspid and was studied by
Bernoulli in 1691, while the 3:1 hypocycloid is known as the deltoid
or tricuspid and was studied by Euler in 1745.
Some more hypocycloids
with ratios of 9:4, 11:2, and 32:5.
Epiroulettes
An epiroulette, also called an epitrochoid, is like an
epicycloid in that one circle is rolling around another circle, but the
drawing point need not be exactly on the edge of the rolling circle. The
drawing point could instead be inside or outside the circle. First, here's a
7:1 epicycloid colored in lavender with three purple epiroulettes line drawn
in the same picture, but with their drawing points beyond the radius of the
rolling circle, so part of these curves lie inside the fixed circle.
Next, here's a 2:1 epicycloid (that is, a nephroid) colored gold with a red epiroulette where the drawing point is within the radius of the rolling circle.
An epiroulette where the rolling circle is the same size is called a
limacon (E. Pascal). Cardioids are special cases of epiroulettes.
And a couple
more epiroulettes
Hyporoulettes
A hyporoulette, also called a hypotrochoid, is like an
epicycloid in that one circle is rolling inside another circle, but, as you
could guess, the drawing point need not be exactly on the edge of the rolling
circle. First a 6:1 hypocycloid with two hyporoulettes with the drawing point
beyond the radius, then a 5:1 hypocycloid with a hyporoulette with the drawing
point within the radius.
And
some more hyporoulettes
Ellipses are hyporoulettes
It may seem surprizing but ellipses are the hyporoulettes, namely the 2:1
hyporoulettes. If the drawing point is at the center of the moving circle,
the resulting hyporoulette is a circle, but otherwise, it's a proper ellipse.
Here are some in this picture.
Roses
Grandi named rhodonea curves (also called rosettes and
rose curves) in 1723. They are just the epirosettes or hyporosettes
passing throught the center of the fixed circle.
And some more roses.
August, 1994