Reconstruction. The question of reconstruction is: How do you reconstruct the phylogenetic tree when all you know are characters of extant species? When there are only a few species, only a few characters, and the number of mutations is small but not too small, then common sense and a little bit of logic does a pretty good job, at least for deciding on the shape of the tree.
As the number of species goes up, and the number of characters goes up, then conflicting data begins to appear. Then common sense and logic are insufficient for the job. Furthermore, the mutation rate may not be high enough to distinguish closely related species, those near the bottom of the tree, but too high to make confident conclusions for reconstructing the top of the tree in order to connect distantly related species. Also, deciding the relative lengths of the lines in the tree, or the equivalent problem of deciding how high to put join the various lines, requires computations and a basis for making computations.
A simplification of the problem. There's a lot of information in the gene sequences, and it's difficult to analyze it all. One way to simplify things is to look at just pairs of species at a time. This will ignore some useful information, but enough will remain to do a pretty good job on reconstructing a phylogenetic tree, and the computations become simpler.
When we look at two species, we have two sequences of characters, and the relevant measure is the number of differences in these two sequences, a measure that we can interpret as the distance between the species. Algorithms that depend only on distances between species are called distance matrix algorithms.
Distances between species. If two species have a small distance between them (as measured by the number of differences in their character sequences), then they have a recent common ancestor; but if they are far apart, then their common ancestor is in the remote past. We can use the distance between the species as a measure of the distance in time since the species diverged. These two distances, the number of character differences and the time since divergence, will be approximately proportional when they're relatively small.
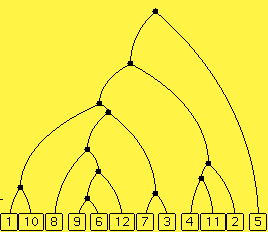
The difference matrix. Here is a model phylogenetic tree with five extant species alongside a matrix. This 5 by 5 matrix results from mutations of 40 irrelevant characteristics each with 4 alternate values. The mutation rate is uniform with a value of 100 mutations per 1000 time units, that is, 0.1 mutations per time unit. The (i,j)th entry in the matrix indicates how many of the 40 characters differ between species i and species j. If two species are not very distant in the tree, then there hasn't been much time for mutations to occur, so the entry in this matrix should be small. If two species are very distant, the entry in the matrix should be large, that is, close to 30, which is 3/4 of the number of characters. You won't see such large entries in the matrix unless you increase the mutation rate or the number of species.
Note that the matrix is symmetric, that is, the (i,j)th entry is the same as the (j,i)th entry. Also, the entries along the diagonal are all 0, denoted here as *, since each (i,i)th entry indicates how many differences between the ith character sequence and itself, which, of course, is 0.
You can play around with the mutation matrix if you like. Press the "mutate" button to request a new set of mutations with the same number of characters, the same number of alternatives per characteristic, and the same mutation rate. You can also change these parameters, and each time you do, you'll get a new set of mutations automatically.
In the next section, we'll look at some algorithms to reconstruct phylogenetic trees from this distance matrix.
Next page: reconstruction algorithms.
Previous page: mutations.
Table of contents: http://aleph0.clarku.edu/~djoyce/java/Phyltree.
David E. Joyce
Department of Mathematics and Computer Science
Clark University
January, 1996