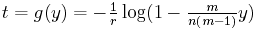
First, we can convert the differences to times. The conversion is given by the formula
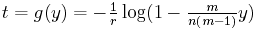
as explained in the page on mutations.
Of course, we might not be able to reconstruct the actual tree, since the mutations are random and need not reflect the actual distances between species. So a better question is: how can we reconstruct the most likely phylogenetic tree? This question could be made precise using statistical theory, but there is no guarantee that the problem is tractable. We can come up with some promising algorithms that should give trees that aren't too far away from the most likely tree.
A solution: the "minimum" reconstruction method.
It seems reasonable that the two species that share the greatest number
of characters are the most closely related. That is, the smallest entry
in the mutation matrix indicates which two species diverged most recently.
Also, the next smallest entry should indicate which two species diverged
just before that. And so forth. That's the idea of the algorithm, but it
needs a little clarification. Suppose species 1 and 2 are closest with 4
differences in their characters, and species 1 and 3 are next closest
with 6 differences. Then since we conclude that species 1 and 2 diverged most recently,
it won't be species 1 and 3 that diverged just before that, rather it will
be the ancestral species of 1 and 2 that diverged from species 3 just before
that.
Here you see a distance matrix (which is actually a mutation matrix based on a hidden model phylogenetic tree) and the reconstructed phylogenetic tree build from this minimum reconstruction method. You should be able to see how that tree can be derived from the matrix.
If you like, you can ask for a different matrix based on different mutations. Note how radically the reconstructed tree varies with each set of mutations. If there are more characters, then you'll see that the reconstructed matrix depends less on which actual mutations occur.
Two other solutions: the "average" and "maximum" methods. There are two algorithms that are very similar to the minimum reconstruction method. They start out exactly the same by joining the two species that share the most characters. To explain these methods, suppose that species 1 and 2 are closest. Name their ancestral species as species 6. With the minimum method, we effectively determined that the distance between species 6 and any other species such as species 3 was the minimum of the distance from 1 to 3 and the distance from 2 to 3. With the maximum method, instead take the distance from species 6 to species 3 to be the maximum of these two distances. And, of course, for the average method, take the average of those two distances.
These three algorithms go by various names. The one using averages is often called "weighted pair group method using arithmetic averages," WPGMS. (There is a closely related algorithm called the "unweighted pair group method using arithmetic averages," UPGMS.) The algorithm using minimum distance is called a "single linkage method," and the one using maximum distance is called a "complete linkage method." All three algorithms use a nearest-neighbor technique to construct a tree.
You can select which of these three reconstruction methods to use in the control panel. It's surprising how similar the trees resulting from these three algorithms are. You can see for yourself by selecting a different algorithm.
Estimating time intervals from distance intervals. When there aren't very many mutations, that is, when the numbers in the difference matrix are small, then you expect time to be proportional to the differences. That is, if one pair of species differ by 3 characters, but another pair of species differ by 6 characters, then we would estimate that the common ancestor of the first pair is twice as recent as the common ancestor of the second pair. That means that the length of the line in the tree (as measured by the elapsed time between the beginning of the line and the end of the line) is about proportional to the number of mutations that occur in the evolving species that that line represents.
That's not quite correct, however. When there is more than one mutation in one character for that species during that time interval, only one mutation can be observed. For short time intervals, double mutations are so rare that it makes no difference, but for very long time intervals, they should be taken into consideration. The algorithm used in these demonstrations assumes that the time intevals are short enough to ignore double mutations. If you turn up the mutation rate very high, you'll see the reconstructed tree squished near the top due to these multiple mutations.
Next page: summary.
Previous page: distances.
Table of contents: http://aleph0.clarku.edu/~djoyce/java/Phyltree.
David E. Joyce
Department of Mathematics and Computer Science
Clark University
January, 1996