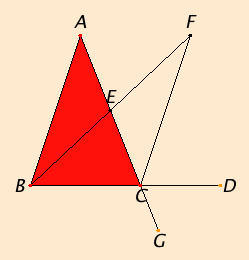
Proposition 16
In any triangle, if one of the sides is produced, then the exterior angle is greater than either of the interior and opposite angles.
Let ABC be a triangle, and let one side of it BC be produced to D.
I say that the exterior angle ACD is greater than either of the interior and opposite angles CBA and BAC.
Bisect AC at E. Join BE, and
produce it in a straight line to F.
Make EF equal to BE, join FC,
and draw AC through to G.
Since AE equals EC, and BE equals EF, therefore the two sides AE and EB equal the two sides CE and EF respectively, and the angle AEB equals the angle FEC, for they are vertical angles. Therefore the base AB equals the base FC, the triangle ABE equals the triangle CFE, and the remaining angles equal the remaining angles respectively, namely those opposite the equal sides. Therefore the angle BAE equals the angle ECF.
But the angle ECD is greater than the angle ECF, therefore the angle ACD is greater than the angle BAE.
Similarly, if BC is bisected, then the angle BCG, that is, the angle ACD, can also be proved to be greater than the angle ABC.
Therefore in any triangle, if one of the sides is produced, then the exterior angle is greater than either of the interior and opposite angles.
Q.E.D.
Guide
In the later proposition I.32, after he invokes the parallel postulate I.Post.5, Euclid shows the stronger result that the exterior angle of a triangle equals the sum of the interior, opposite angles.
Elliptic geometry
There are geometries besides Euclidean geometry. Two of the more important geometries are elliptic geometry and hyperbolic geometry, which were developed in the nineteenth century. The first 15 propositions in Book I hold in elliptic geometry, but not this one. (For more on hyperbolic geometry, see the note after Proposition I.29.)
Plane elliptic geometry is closely related to spherical geometry, but it differs in that antipodal points on the sphere are identified. Thus, a “point” in an elliptic plane is a pair of antipodal points on the sphere. A “straight line” in an elliptic plane is an arc of great circle on the sphere. When a “straight line” is extended, its ends eventually meet so that, topologically, it becomes a circle. This is very different from Euclidean geometry since here the ends of a line never meet when extended.
|
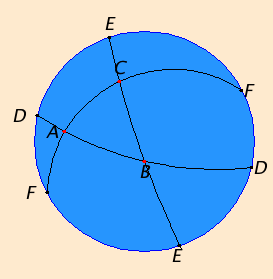
The illustration on the right shows the stereographic projection of one hemisphere. Since only one hemisphere is displayed, each “point” is represented by one point except those “points” such as D, E, and F on the blue bounding great circle which appear twice.
A “triangle” in elliptic geometry, such as ABC, is a spherical triangle (or, more precisely, a pair of antipodal spherical triangles). The internal angle sum of a spherical triangle is always greater than 180°, but less than 540°, whereas in Euclidean geometry, the internal angle sum of a triangle is 180° as shown in Proposition I.32.
Elliptic geometry satisfies some of the postulates of Euclidean geometry, but not all of them under all interpretations. Usually, I.Post.1, to draw a straight line from any point to any point, is interpreted to include the uniqueness of that line. But in elliptic geometry a completed “straight line” is topologically a circle so that any pair of points on it divide it into two arcs. Therefore, in elliptic geometry exactly two “straight lines” join any two given “points.”
|
|
Also, I.Post.2, to produce a finite straight line continuously in a straight line, is sometimes interpreted to include the condition that its ends don’t meet when extended. Under that interpretation, elliptic geometry fails Postulate 2.
Elliptic geometry fails I.Post.5, the parallel postulate, as well, since any two “straight lines” in an elliptic plane meet. That is, any two great circles on the sphere meet at a pair of antipodal points.
Finally, a completed “straight line” in the elliptic plane does not divide the plane into two parts as infinite straight lines do in the Euclidean plane. A completed “straight line” in the elliptic plane is a great circle on the sphere. Any two “points” not on that “straight line” include two points in the same hemisphere, and they can be joined by an arc that doesn’t meet the great circle. Therefore two “points” lie on the same side of the completed “straight line.”
The proof of this particular proposition fails for elliptic geometry, and the statement of the proposition is false for elliptic geometry. In particular, the statement “the angle ECD is greater than the angle ECF” is not true of all triangles in elliptic geometry. The line CF need not be contained in the angle ACD. All the previous propositions do hold in elliptic geometry and some of the later propositions, too, but some need different proofs.
Use of Proposition 16
This proposition is used in the proofs of the next two propositions, a few others in this book, and a couple in Book III.