Proposition 27
If a straight line falling on two straight lines makes the alternate angles equal to one another, then the straight lines are parallel to one another.
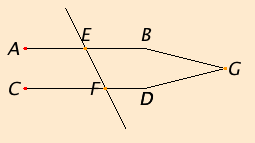
Let the straight line EF falling on the two straight lines AB and CD make the alternate angles AEF and EFD equal to one another.
I say that AB is parallel to CD.
If not, AB and CD when produced meet either in the direction of B and D or towards A and C.
Let them be produced and meet, in the direction of B and D, at G.
Then, in the triangle GEF, the exterior angle AEF equals the interior and opposite angle EFG, which is impossible.
Therefore AB and CD when produced do not meet in the direction of B and D.
Similarly it can be proved that neither do they meet towards A and C.
But straight lines which do not meet in either direction are parallel. Therefore AB is parallel to CD.
Therefore if a straight line falling on two straight lines makes the alternate angles equal to one another, then the straight lines are parallel to one another.
Q.E.D.
Note that Euclid does not consider two other possible ways that the two lines could meet, namely, in the directions A and D or toward B and C.
This little table summarizes the logical relations between similarly looking statements.
Although the contrapositive is logically equivalent to the statement, Euclid always proves the contrapositive separately using a proof by contradiction and the original statement. Similarly, the inverse is proved using the converse. Sometimes all four statements appear in separate propositions as in propositions X.5 through X.8. Other times the four appear as four statements in one proposition as in X.9. More often than not, however, the contrapositive and inverse make no appearance, and, of course, the converse only appears when it can be proved.