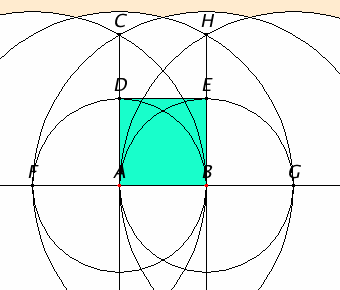
Proposition 46
Let AB be the given straight line.
It is required to describe a square on the straight line AB.
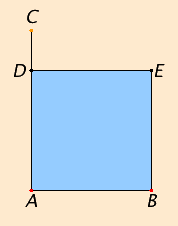
Draw AC at right angles to the straight line AB from the point A on it. Make AD equal to AB. Draw DE through the point D parallel to AB, and draw BE through the point B parallel to AD.
Then ADEB is a parallelogram. Therefore AB equals DE, and AD equals BE.
But AB equals AD, therefore the four straight lines BA, AD, DE, and EB equal one another. Therefore the parallelogram ADEB is equilateral.
I say next that it is also right-angled.
Since the straight line AD falls upon the parallels AB and DE, therefore the sum of the angles BAD and ADE equals two right angles.
But the angle BAD is right, therefore the angle ADE is also right.
And in parallelogrammic areas the opposite sides and angles equal one another, therefore each of the opposite angles ABE and BED is also right. Therefore ADEB is right-angled.
And it was also proved equilateral.
Therefore it is a square, and it is described on the straight line AB.