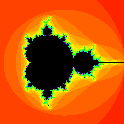
Julia and Mandelbrot Sets
Help for the Mandelbrot and Julia Set Explorer
For background on Julia and Mandelbrot sets, see the introduction.
Getting Julia sets corresponding to various points in the Mandelbrot set
To begin with, you only see one image, the Mandelbrot set as a subset of the complex plane. The form is initially set so that if you click on that image, you'll get a second image on the form,
namely, the Julia set determined by the particular point in the complex plane that you clicked at.
If you continue to click on the Mandelbrot set, the Julia set image will be replaced by other Julia sets. You can pretty easily get a pretty good idea how the Julia sets are related to the
Mandelbrot set.
Selecting the parameter plane for the Mandelbrot set
There are various ways you can view the Mandelbrot set. Typically, and by default, the µ plane is chosen. Then the iterating function is f(z) =
z2 - µ.
The set of quadratic functions can be parameterized in different ways. Another common parameter is lambda, and the iterating function is f(z) = lambda z(1-z).
The relation between lambda and µ is that µ = lambda2/4 - lambda/2. Geometrically, converting from µ to lambda doubles the plane around the singularity of the cardioid which
converts the cardioid into a pair of circles, and all the other circles remain circles.
When 1/µ is displayed, the image becomes a teardrop shape. The original cardioid is transformed into the outside of the teardrop.
When 1/(µ+0.25) is displayed, the image appears parabolic. The original cardioid is transformed into the outside of the parabola.
When 1/lambda is displayed, the image appears as a circle, or, better stated, as a crescent, since one of the two primary circles in the lambda plane is converted to the outside of the circle, and the
other is converted to the interior of a smaller circle inside that circle.
When 1/(lambda-1) is displayed, the image appears as an infinite strip. The two circles of the lambda plane are converted to the two sides outside the strip.
When 1/(µ-1.40115) is displayed, the cardioid is turned around and distorted a bit, but the real difference is that the sequence of circles attached to the right of the cardioid are expanded,
each bigger then the previous. Their radii increase to infinity instead of decrease to 0.
Magnifying the images
There are two ways you can get more detail about an image. Rather than looking at the whole Mandelbrot or Julia set, you can magnify a piece of it. If you click on the Julia set, you'll get a
magnified piece of that Julia set centered at your click point. Initially, the magnification factor is 3, but you can change that if you want to. The actual image size won't change, however, so the
square of the complex plane being displayed in the image will be cut down by a factor of 3 in both dimensions.
You can magnify a piece of the Mandelbrot set, too. Just press the clickbox labelled "magnify the Mandelbrot set" before clicking on the Mandelbrot image. You'll also get a Julia set at the same
time unless you press the clickbox labelled "get a Julia set".
You can also change the size of the image you get. To begin with the images are squares 300 pixels on a side. You can change that square to any size rectangle you like. The new shape will be sent
on your next image request. That gives you another way to magnify an image. Please note that big images take noticeably longer to compute than small images.
Iteration limits
The "escape" algorithm for computing the Mandelbrot and Julia sets depends on iterating a function some number of times. Mathematically, if iterating the function infinitely many times doesn't lead
to infinity, then the initial point lies in the set (either Mandelbrot or Julia). Iterating a function infinitely many times takes a while, as you can imagine :) So there has to be a limiting
number of iterations that will count as infinity. The image actually displayed, then, is not the set you're looking for, but only an approximation. The initial maximum number of iterations is 50,
but as you start going deeper into the sets, you'll want to up that limit. Please note that the larger this number is, the longer it takes to compute the image.
Image rendition
If you don't have a color screen or would like greyscale images for some other reason, they're available.
Also, to increase the changes in colors (either for color or grayscale images) you might prefer to wrap through the colors more than once. The "zebra" option produces a black and white image where
levels alternate between black and white.
You can add some detail to images by changing the "escape" conditions for the algorithm. The usual condition is that the iterate of the function eventually gets outside a sufficiently large circle.
The mathematics then guarantees further iterates will go off to infinity. But if you prefer, you can change the circle into a square. The boundaries between levels will become scalloped instead of
smooth. You can also "feather" the image, either with a square or a circular boundary. Feathering adds black so that the levels look something like they're colored with feathers.
Downloading the images
On a lot of web pages, the images have been set so that if you click on them, either that image or a larger one will be sent for you to view on an external viewer. The Mandelbrot and Julia images are
clickable images, and the click information is used for a different purpose. But down toward the bottom of this form, there are references to download the images.
Recently created images
The files containing the created images are purged frequently, but recent ones may be accessed via their index if you like. The gifs as well as the html's are accessible.
September, 1994. © 1994.
David E. Joyce

Department of Mathematics and Computer Science
Clark University
Worcester, MA 01610
These pages are located at http://aleph0.clarku.edu/~djoyce/julia/julia.html


